Two functions are defined as under, f(x)={x+1x≤12x+11<x≤2 g(x)={x2−1≤x<2x+22≤x≤3
Find fog and gofSolution in Bengali
We have f(g(x))={g(x)+1,g(x)≤02g(x)+1,1<g(x)≤2
Here, g(x) is argument of the function f(g(x))
So, we draw the graph of y=g(x).
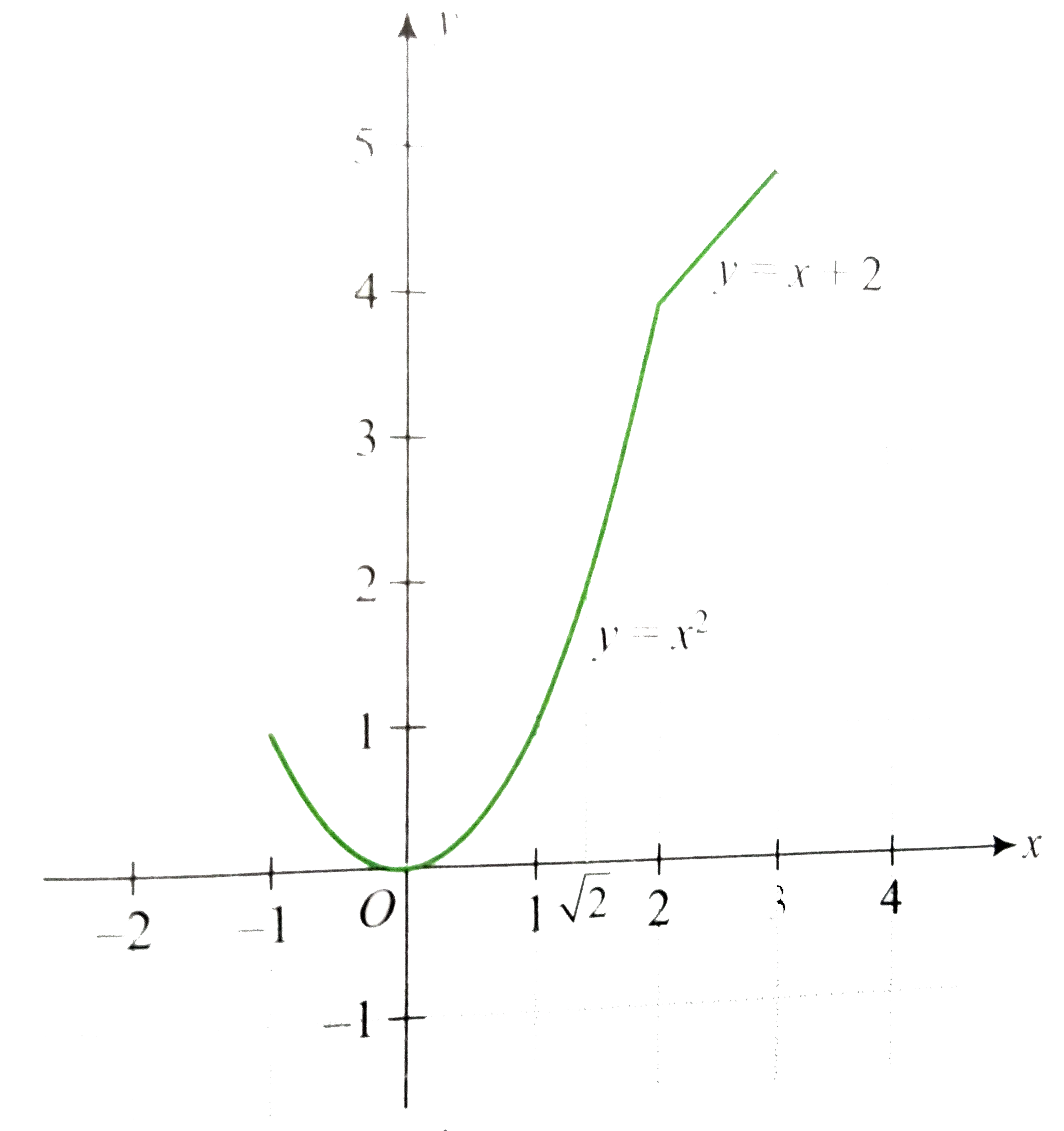
From the graph it is clear that g(x)≤1,∀x∈[−1,1]
and 1<g(x)≤2,∀x∈(1,√2]
⇒f(g(x))={x2+1,−1≤x≤12x2+1,1<x≤√2
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 6
View SolutionIf f(x)=√x(x>0)andg(x)=x2−1 are two real functions, find fogandgof is fog=gof?
View SolutionTwo functions are defined as under : f(x)={(x+1, x le 1), (2x+1, 1 < x le 2):} and g(x)={(x^2, -1 le x le 2), (x+2, 2 le x le 3):} Find fog and gof
View SolutionIf f(x)=√x+3 and g(x)=x2+1 be two real functions, then find fog and gof .
View SolutionIf f and g are two functions from R to R which are defined as f(x)=x2+x+1andg(x)=2x−1 for each x∈R, then show that (fog) (x) ≠ (gof) (x).
View Solutionयदि f और g, R से R में दो फलन हैं, जो प्रत्येक x∈R के लिये f(x)=x2+x+1 और g(x)=2x−1 से परिभाषित हैं । दिखाइए कि (fog)(x)≠(gof)(x).
View Solutionयदि f:R→R और g:R→R,f(x)=x+2 और g(x)=2x2+5 द्वारा परिभाषित है तो fog और gof ज्ञात कीजिए ।
View Solutionयदि फलन f:R→R,f(x)=x2+2 और g:R→R,g(x)=xx−1 द्वारा परिभाषित हो , तो fog और gof ज्ञात कीजिए ।
View SolutionIf f,g:R→R be two functions defined as f(x)=|x|+x and g(x)=|x|−x. Find fog and gof. Hence find fog(−3), fog(5) and gof(−2).
View SolutionTwo functions are defined as under : f(x)={x+1x≤12x+11<x≤2 and g(x)={x2−1≤x≤2x+22≤x≤3 Find fog and gof
View SolutionIf f(x)=√x(x>0)andg(x)=x2−1 are two real functions, find fogandgof is fog=gof?
View SolutionIf f(x)=√x(x>0)andg(x)=x2−1 are two real functions, find fogandgof is fog=gof?
View SolutionIf f(x)=√x+3 and g(x)=x2+1 be two real functions, then find fog and gof .
View SolutionIf f,g,:R−R be two functions defined as f(x)=|x|+x and g(x)=|x|−x,∀xR, Then find fog and gof. Hence find fog(−3),fog(5) and gof(−2).
View Solutionf and g are real valued function f(x)=x2+x+7,x∈Randg(x)=5x−3,x∈R . Find fog and gof. Also find (fog)(2) and (gof)(1).
View Solution
