Let O be the circumcentre and H be the orthocentre of an acute angled triangle ABC. If A>B>C, then show that Ar(ΔBOH)=Ar(ΔAOH)+Ar(ΔCOH)Solution in Bengali

From the figure, we have
∠OAH=A−2(90∘−B)=B−C
Similarly, ∠OBH=A−C
and ∠OCH=A−B
Also, AH=2RcosA,BH=2RcosB,CH=2RcosC
Ar(ΔAOH)=12(R)(2RcosA)sin(B−C)
=R2cos(B+C)sin(C−B)
=R22(sin2C−sin2B)
Similarly, Ar(ΔBOH)=R22(sin2C−sin2A)
and Ar(ΔCOH)=R22(sin2B−sin2A)
Clearly, AR(ΔAOH)+Ar(ΔCOH)=Ar(ΔBOH)
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Illustration
86 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE PUBLICATIONCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.1
12 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE PUBLICATIONCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE )
8 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - All Questions
1119 Videos
Similar Questions
If an a triangle ABC,a=3band B−A=900, then find the value of tanA
View SolutionFind the value of a2+b2+c2R2 in any right-angled triangle.
View SolutionLet Sk,k=1,2,….100 denote the sum of the infinite geometric series whose first term is k−1K! and the common
ration is 1k then the value of (100)2100!+Σ100k=1|(k^2-3k+1)S_k| is ____________
View SolutionIf the function f:[1,∞)→[1,∞) is defined by f(x)=2x(x−1), then find f−1(x)
View SolutionIn Delta ABC,AD and BE are altitudes.Prove that (ar(Delta DEC))/(ar(Delta ABC))=(DC^(2))/(AC^(2))
View Solutionकिसी त्रिभुज ABC की मधिकाएँ CD और BE एक दूसरे को O पर कटती है , तो अनुपात Ar △ODE:Ar △ABC किसके बराबर होगा ?
View SolutionLet O be the circumcentre and H be the orthocentre of an acute angled triangle ABC. If A>B>C, then show that Ar(ΔBOH)=Ar(ΔAOH)+Ar(ΔCOH)
View SolutionIt is given that ΔABC~ΔPRQandBCQR=23 then ar(ΔPQR)ar(ΔABC)=?
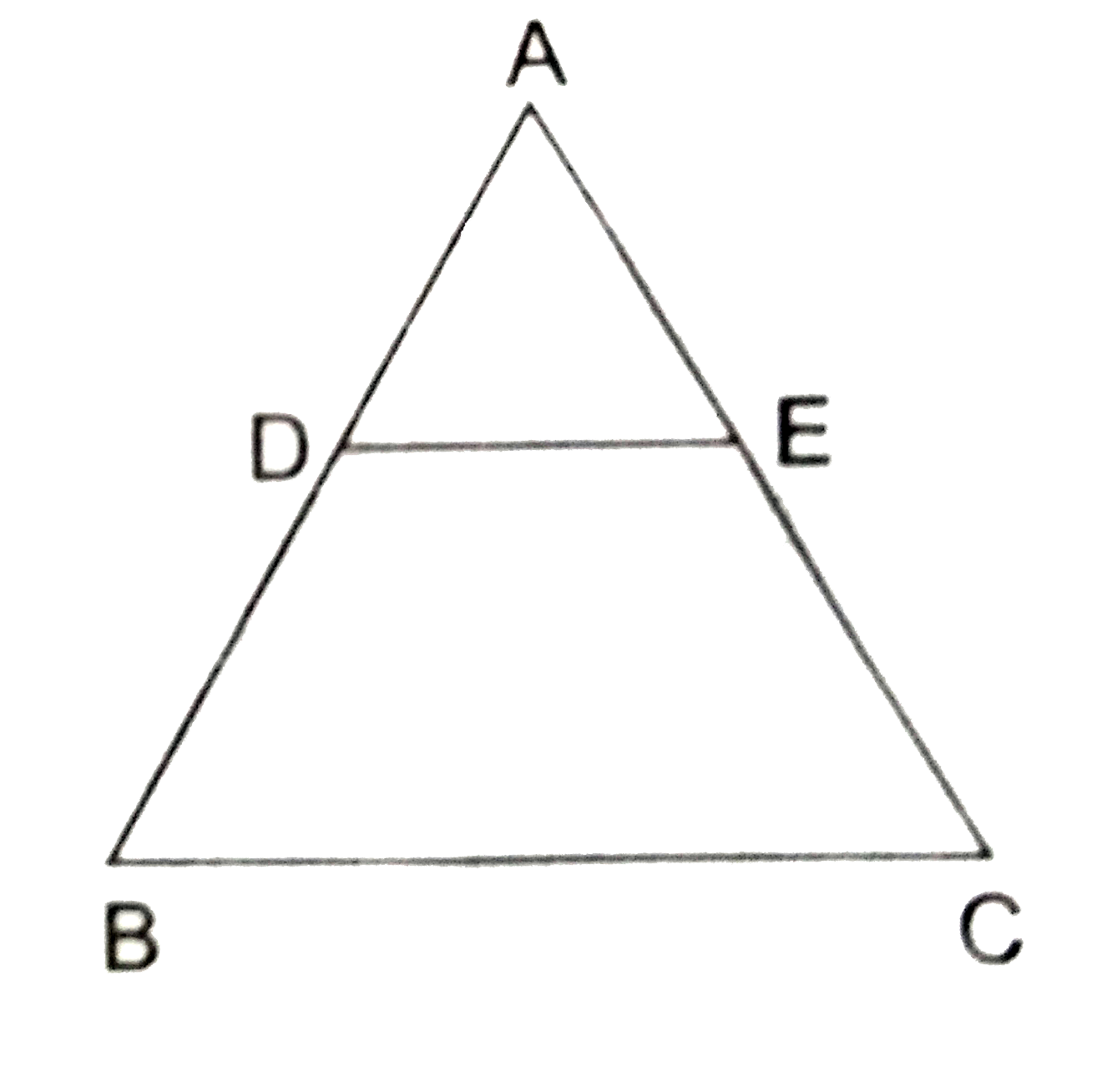
View SolutionIn an equilateral ΔABC,D is the midpoint of AB and E is the midpoint of AC. Then, ar(ΔABC):ar(ΔADE)=?
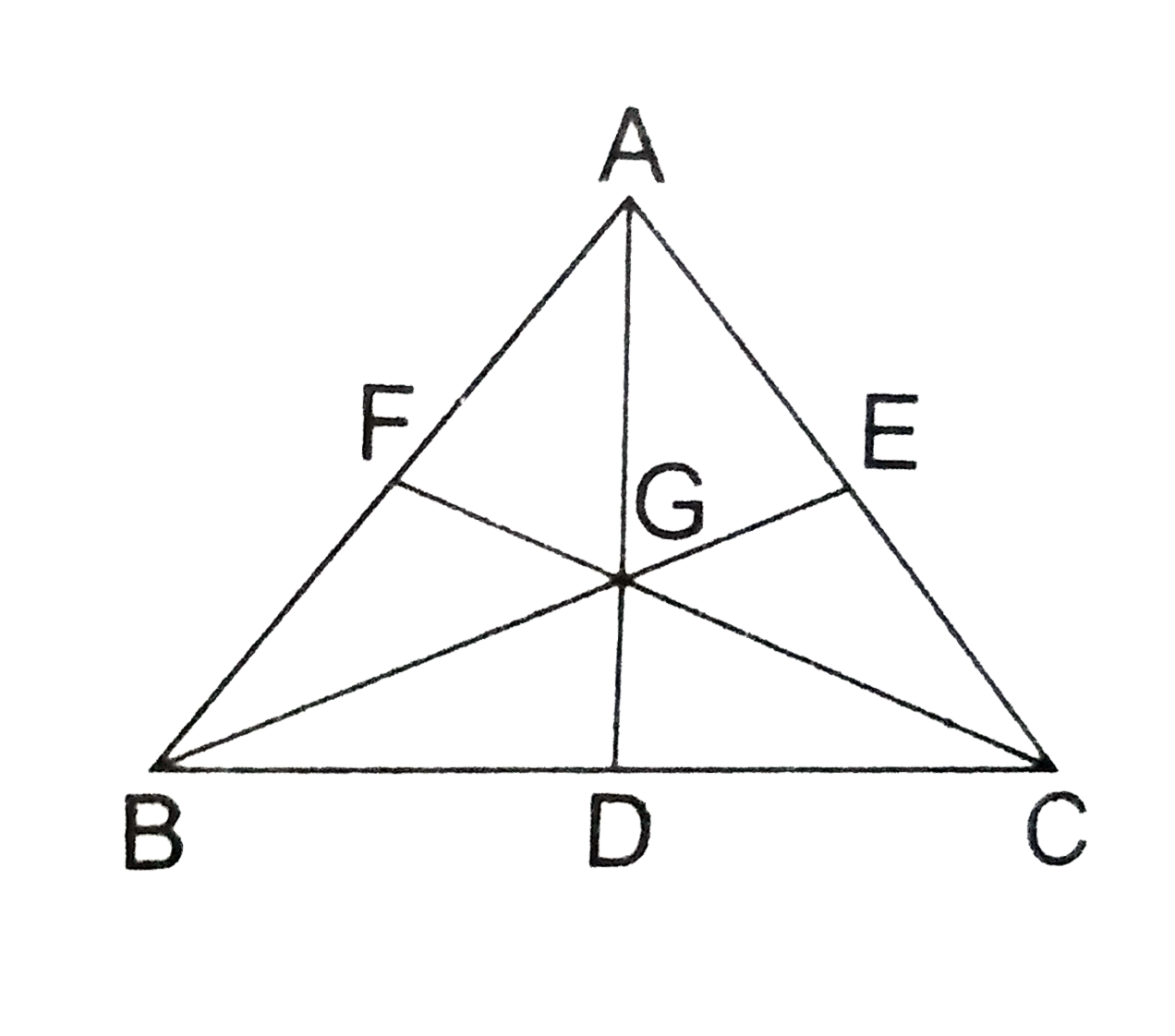
View SolutionIf the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
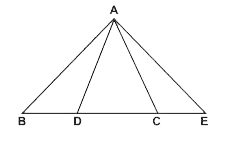
View SolutionIn the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
View SolutionIts vertices A, B, C and D are joined by a point O located in the interior of a rectangle ABCD. Prove that ar ( Delta AOD ) + ar ( Delta BOC ) = ar ( Delta AOB ) +ar(Delta COD )
View SolutionDelta ABC A point D on BC is such that BD = ( 1)/( 3) DC Show that ar( Delta ABD ) = ( 1)/( 4) ar ( Delta ABC )
View SolutionIf ΔABC~ΔPQR with BCQR=13, then find arΔPRQarΔBCA ?
View SolutionΔABC and ΔBDC are on the same base BC. Prove that ar(ΔABC)ar(ΔDBC)=AODO
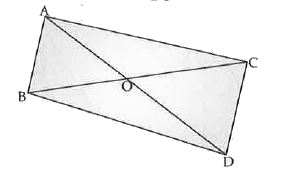
View Solution
