Consider
∫x3+3x2+2x+1√x2+x+1dx
=(ax2+bx+c)√x2+x+1+λ∫dx√x2+x+1
Now, match the following lists and then choose the correct code.

Codes:
abcd(1)qpsr(2)spqr(3)rqps(4)qsprSolution in Bengali
The correct Answer is:4
∫x3+3x2+2x+1√x2+x+1dx
=(ax2+bx+c)√x2+x+1+λ∫dx√x2+x+1
Differentiating both side, we get
x3+3x2+2x+1√x2+x+1=(ax2+bx+c)(2x+1)2√x2+x+1+(2ax+b)√x2+x+1+λ1√x2+x+1
=6ax3+(5a+4b)x2+(4a+3b+2c)x+(c+2b+2λ)2√x2+x+1
Now, compare coefficients on both sides and solve equations.
Topper's Solved these Questions
- INDEFINITE INTEGRATIONBOOK - CENGAGE PUBLICATIONCHAPTER - INDEFINITE INTEGRATIONEXERCISE - EXERCISES (Numerical Value Type)
10 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGE PUBLICATIONCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Archives JEE MAIN (Single Correct Answer Type)
7 Videos
- INDEFINITE INTEGRATIONBOOK - CENGAGE PUBLICATIONCHAPTER - INDEFINITE INTEGRATIONEXERCISE - Exercises (Linked Comprehension Type)
17 Videos
- HYPERBOLABOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE
2 Videos
- INEQUALITIES AND MODULUSBOOK - CENGAGE PUBLICATIONCHAPTER - INEQUALITIES AND MODULUSEXERCISE - Single correct Answer
21 Videos
Similar Questions
Let f(x)=∫xsinx(1+xcosx.lnx+sinx)dxandf(π2)=π24. Then the value of |cos(f(π))| is____
View SolutionIf the integral ∫5tanxtanx−2dx=x+aIn|sinx−2cosx|+k, then a is equal to
View Solutiony=f(x) is a polynomial function passing through point (0, 1) and which increases in the intervals (1,2)and(3,∞) and decreases in the intervals (∞,1)and(2,3).
If f(1)=−8, then the value of f(2) is
View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
View SolutionIf f(x)=ax2+bx+c and f(−1)≥−4, f(1)≤0 and f(3)≥5, then the least value of a is
View SolutionIf I=∫sinx+sin3xcos2xdx=Pcosx+Qlog|f(x)|+R, then (a)P=12,Q=−34√2 (b) P=14,Q=1√2 (c)f(x)=√2cosx+1√2cosx−1 (d) f(x)=√2cosx−1√2cosx+1
View Solutionint(dx)/(sqrt(x+7)-root(4)(x+7))=P sqrt(x+7)+Q(x+7)^((1)/(4))+R ln|(x+7)^((1)/(4))-1|+ then (A)P!=Q!=R(B)Q=R(C)P!=Q(D)P+Q+R=10
View SolutionMatch the following lists (where [x] represents the greatest integer function) and then choose the correct code.
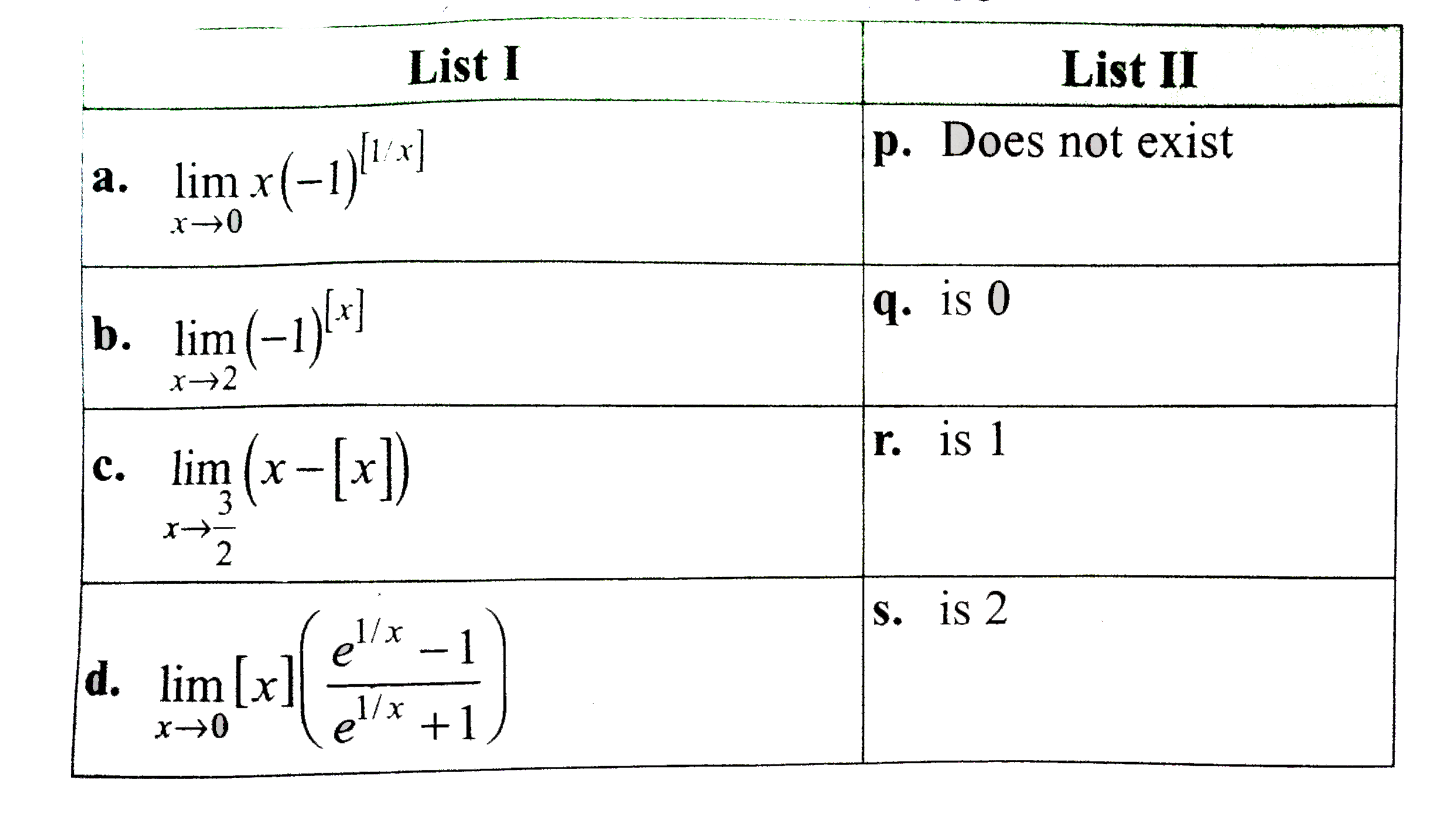
Codes :
a b c d(1)s r q p(2)q p s p(3)s r p q(4)p p q r
View SolutionConsider
∫x3+3x2+2x+1√x2+x+1dx
=(ax2+bx+c)√x2+x+1+λ∫dx√x2+x+1
Now, match the following lists and then choose the correct code.

Codes:
abcd(1)qpsr(2)spqr(3)rqps(4)qspr
View SolutionIf y = 11+xp−r+xq−r+11+xp−q+xr−q+11+xq−p+xr−p,thendydx=
View Solution√xp−q√xq−r√xr−p=1
View Solution∫(x3−1)dxx4√6x6−4x3+2(x>0)=√6x6−4x3+PQxR+c then P+Q−R is equal to
View Solution∫(x2+1)dxx√x2+2x−1√1−x2−x=Psin−1√x−1x+Q+C then PQ is equal to
View Solution∫(x2+1)dxx√x2+2x−1√1−x2−x=Psin−1√x−1x+Q+C then PQ is equal to
View SolutionMatch the following lists (where [x] represents the greatest integer function) and then choose the correct code.

Codes :
a b c d(1)s r q p(2)q p s p(3)s r p q(4)p p q r
View SolutionConsider
∫x3+3x2+2x+1√x2+x+1dx
=(ax2+bx+c)√x2+x+1+λ∫dx√x2+x+1
Now, match the following lists and then choose the correct code.

Codes:
abcd(1)qpsr(2)spqr(3)rqps(4)qspr
View Solution
