Two points PandQ are given. R is a variable point on one side of the line PQ such that ∠RPQ−∠RQP is a positive constant 2α. Find the locus of the point R.Solution in Bengali
Let R≡(x1,y1).
Also , let, ∠RPM=thetand∠RQM=ϕ.
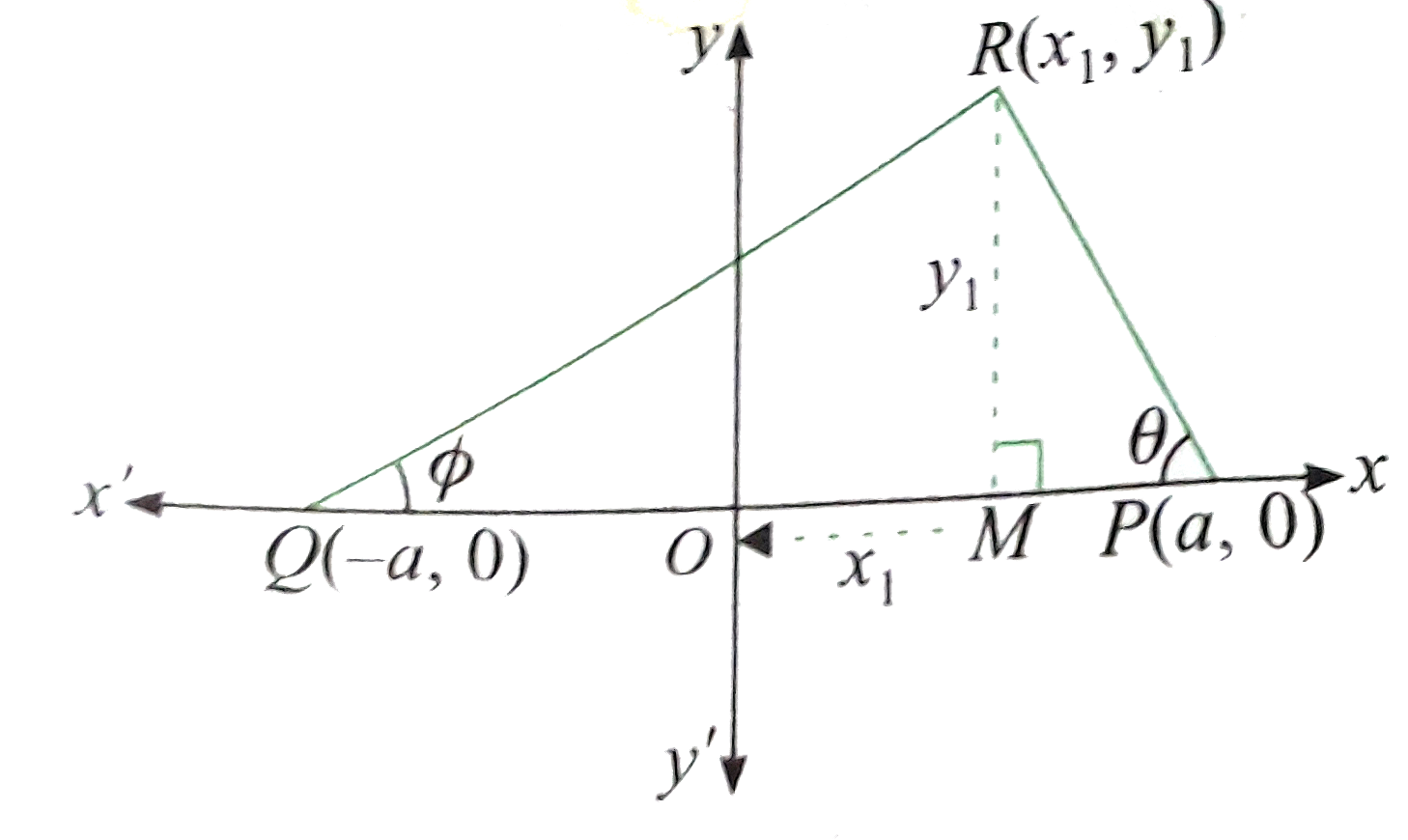
In ΔRMP,tanθ=RMMP=y1a−x1
In ΔRQM,tanθϕ=RMQM=y1a+x1
But given ∠RPQ−anl≥RQP=2α (constant).Therefore, θ−ϕ=2α
or tan(θ−ϕ)=tan2α
or tanθ−tanθ1+tanθtanθ=tan2α
or y1a−x1−y1a+x11+y1a−x1y1a+x1=tan2α
or 2x1y1a2=x21+y21=tanα
or a2−x21+y21=2x1y1cot2α
or x21−y21+2x1y1cot2α=a2
Hence, the locus of the point R(x1,y1) is x2−y2+2xycot2α=a2
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.64
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.65
1 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Illustration1.62
1 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
If the coordinates of a variable point P are (acosθ,bsinθ), where θ is a variable quantity, then find the locus of P.
View SolutionFind the locus of the point (t2+t+1,t2−t+1),t∈R.
View SolutionAB is a variable line sliding between the coordinate axes in such a way that A lies on the x-axis and B lies on the y-axis. If P is a variable point on AB such that PA=b,Pb=a , and AB=a+b, find the equation of the locus of P.
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionTwo points P(a,0) and Q(-a,0) are given,R is a variable on one side of the line PQ such that /_RPQ-/_RQP is a positive constant 2 alpha. FInd the locus of point R .
View SolutionTwo points P(a,0) and Q(-a,0) are given. R is a variable point on one side of the line PQ such that ∠RPQ−∠RQP is a positive constant 2α. Find the locus of the point R.
View SolutionGiven P=(1,0) and Q=(-1,0) and R is a variable point on one side of the line PQ such that /_RPQ-/_RQP=(pi)/(4). The locus of the point R is
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionTwo points P(a,0) and Q(-a,0) are given. R is a variable point on one side of the line PQ such that ∠RPQ−∠RQP is a positive constant 2α. Find the locus of the point R.
View SolutionIf P is any point on the plane lx+my+nz=pandQ is a point on the line OP such that OP.OQ=p2 , then find the locus of the point Q.
View SolutionIf P is any point on the plane lx+my+nz=pandQ is a point on the line OP such that OP.OQ=p2 , then find the locus of the point Q.
View SolutionGiven two points P and Q , find how many line segments do they deter-mine. Name the line segments determined by the three collinear points P, Q and R.
View SolutionIn Figure, PQRS is a quadrilateral and T and U are respectively points on PS and RS such that PQ=RQ, ∠PQT=∠RQU and ∠TQS=∠UQS. Prove that QT=QU.
View SolutionIn Figure, PQ>PR.QS and RS are the bisectors of ∠Q and ∠R respectively. Prove that SQ>SR.
View SolutionGiven P=(1,0) and Q=(−1,0) and R is a variable point on one side of the line PQ such that ∠RPQ−∠RQP=π4. The locus of the point R is
View Solution
