Question

Draw the graph of the function $f\left(x\right)=x-|x^2-x|-1\le x\le 1$, where $[\cdot ]$ denotes the greatest integer function. Find the points of discontinuity and non-differentiability.

Explanation

Here, `" "f(x)= |(x+ (1)/(2))[x]|, -2 le x le 2`
`rArr" "f(x)= {{:(|(x+(1)/(2))(-2)|",",, -2le xlt -1),(|(x+(1)/(2))(-1)|",",,-1le xlt 0), (|(x+ (1)/(2))(0)|",",,0 le x lt1),(|(x+ (1)/(2))(1)|",",,1lexlt 2),(|(3)/(2)*2|",",,x=2):}`
`rArr" "={{:(-(2x+1)",",,-2lexlt-1),(-(x+1//2)",",,-1le x lt -1//2),((x+1//2)",",,-(1)/(2)le x lt 0),(0",",,0le x lt 1),(x+ (1)/(2)",",,1 le x lt 2),(3",",,x=2):}`
The graph of the function is as shown in the following figure.

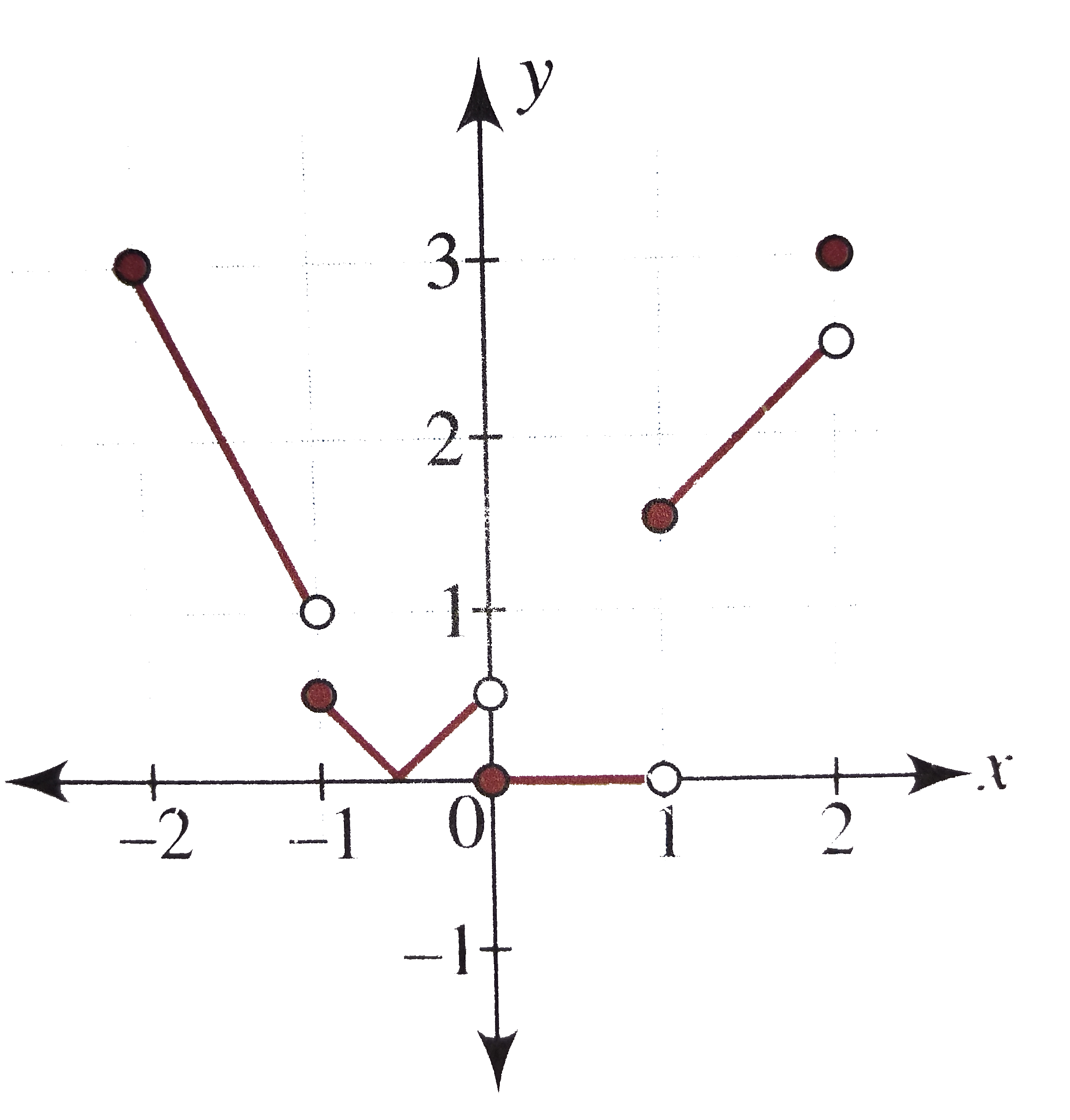
From the figure, `f(x)` is not continuous as `x= { -1, 0, 1, 2}` as at these points, the graph is broken and `f(x)` is not differentiable.
At `x= {-1, (-1)/(2), 0, 1, 2}` as at `{-1, 0, 1, 2}`, the graph is broken and `x=-1//2`, there is a sharp edge.