Find the greatest value of f(x)=12ax−x2−5a2∈[−3,5] depending upon the parameter a.Solution in Bengali
We have f(x)=12ax−x2−5a2=1−4a2−(x−a)2
Let us first draw the graph of y=f(x).
Clearly, f(x) is continuous ∀x∈R.
f(0)=1−5a2. Hence the graph cuts the y-axis at its negative side.
f(a−x)=f(a+x). Hence the graph is symmetrical about the line x = a.
Clearly, y=f(x) is minimum when x=a,f(a)=1−4a2
Also the graph has horizontal asymptote y = 0 (x-axis).
Graph has no vertical or oblique asymptote.
Further f(x)<0,∀x∈R.
From the above information, the graph of y=f(x) is as shown in the following figure.
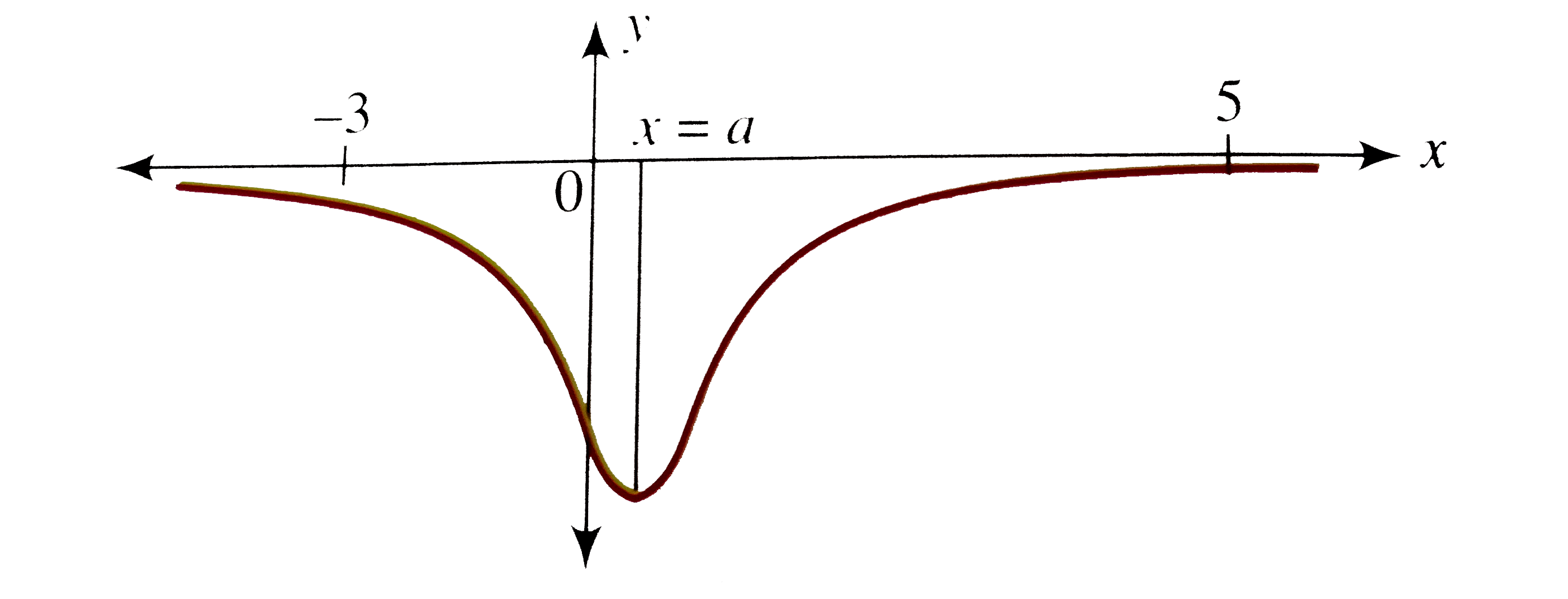
If a=1 (mid point ofx−3andx=5), the greatest value is f(5)=f(−3).
If a<1,fmax(x)=f(5)=−15(a2−2a+5)
and if a>1,fmax(x)=f(−3)=−15a2+6a+9
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises17videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - ILLUSTRATION78videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
02:55View SolutionPlot y=|x|,y+x−2∣,andy=|x|2∣
04:30View SolutionDraw the graph of y=1(1/x).
05:55View SolutionFind the greatest value of f(x)12ax−x2−5a2∈[−3,5] depending upon the parameter a.
04:49View SolutionFind the greatest and least values of f(x)=x^(2)log x in [1,e]
00:50View SolutionFind the greatest and least values of function f(x)={−x, −1≤x<02−(x−1)2, 0≤x≤2
03:19View SolutionFind greatest and least values of f(x)=a2x+b21−x, x ∈(0, 1)(a,b>0).
04:13View SolutionFind each of the products: (−5a)× (−10a2)×(−2a3)
01:12View SolutionThe expression (a-2)x^(2)+2(2a-3)x+(5a-6) is positive for all real value of x, then
05:36View SolutionThe greatest value of f(x)=(x^(2)+x+2)/(x^(2)+x+1) will be
05:10View Solutiona का मान ज्ञात करें ताकि
x2−3x+5a,x−2 से विभाज्य हो जाये।05:33View SolutionThe greatest value of the function f(x)=x2log1x is-
03:03View SolutionFind the values of parameter a for which the function.
y=ax3+3x2+(2a+1)x+1000
is strictly decreasing for all real values of x.04:10View SolutionFind the greatest value of f(x)=12ax−x2−5a2∈[−3,5] depending upon the parameter a.
02:36View SolutionFind the greatest value of f(x)12ax−x2−5a2∈[−3,5] depending upon the parameter a.
08:08View SolutionFind the least value of 'a' such that the function f(x)=x2+ax+1 is increasing on [1, 2] . Also, find the greatest value of 'a' for which f(x) is decreasing on [1, 2] .
06:46View Solution
