Let f(x)=1+4x−x2,∀x∈R
g(x)=max{f(t),x≤t≤(x+1),0≤x<3}=min{(x+3),3≤x≤5} Verify conntinuity of g(x), for all x∈[0,5] Solution in Bengali
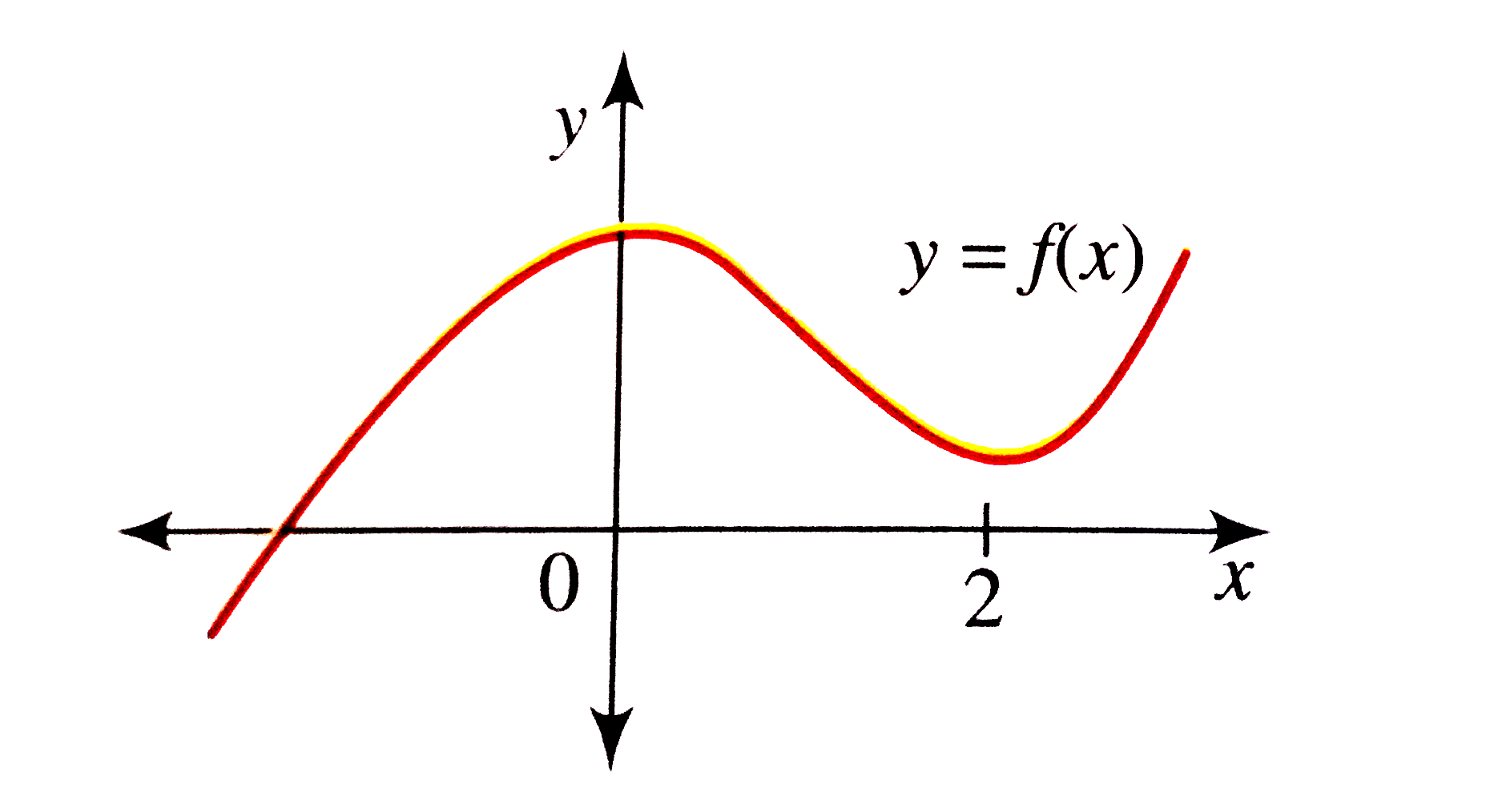
f(x)=x3−3x2+6
If f'(x)=3x2−6x=0, then x=0,2 are the critical points of f(x).
x=0 is the point of local maxima and x=2 is the point of local minima.
Clearly, f(x) is increasing in (−∞,0) and (2,∞) and decreasing in (0,2).
Case 1 : x+2≤0⇒x≤−2
⇒ g(x)=f(x+2),−3≤x≤−2
Case 2: x+1<0 and 0<x+2<2
x<−1 and −2<x<0
i.e., −2<x<−1 ∴g(x)=f(0)
Case 3: 0≤x+1,x+2≤2
⇒−1≤x≤0,g(x)=f(x+1)
⇒g(x)=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩f(x+2), −3≤x<−2f(0), −2≤x<−1f(x+1), −1≤x<01−x, 0≤x<1
Topper's Solved these Questions
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
17 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - ILLUSTRATION
78 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
View SolutionPlot y=|x|,y+x−2∣,andy=|x|2∣
View SolutionDraw the graph of y=1(1/x).
View SolutionLet f(x)=f_1(x)-2f_2 (x), where ,where f_1(x)={((min{x^2,|x|},|x|le 1),(max{x^2,|x|},|x| le 1)) and f_2(x)={((min{x^2,|x|},|x| lt 1),({x^2,|x|},|x| le 1)) and let g(x)={ ((min{f(t):-3letlex,-3 le x le 0}),(max{f(t):0 le t le x,0 le x le 3})) for -3 le x le -1 the range of g(x) is
View SolutionLet f(x)=x3−3x2+6∀x∈R and g(x)={(max.f(t),x+1≤t≤x+2,−3≤x≤0),(1−x for x≥0)
Then find y=g(x) for x∈[−3,1].
View SolutionLet f(x)=f1(x)−2f2(x), where
where f(x)={min{x2,|x|},|x|≤1max{x2,|x|},|x|>1
and f2(x)={min{x2,|x|},|x|>1max{x2,|x|},|x|≤1
and let g(x)={min{f(t):−3≤t≤x, −3≤x<0}max{f(t):0≤t≤x, 0≤x≤3}
For x∈(−1,0),f(x)+g(x) is
View SolutionLet f(x)=x3−x2+x+1andg(x) be a function defined by g(x)={Max{f(t):0≤t≤x}0≤x≤13−x1≤x≤2 Then, g(x) is
View SolutionLet f(x)=x3−x2+x+1andg(x)={maxf(t),0≤t≤xfor0≤x≤13−x,1<x≤2 Then, g(x) in [0, 2] is
View SolutionLet f(x)=1+4x−x2,∀x∈R g(x)=max{f(t),x≤t≤(x+1),0≤x<3min{(x+3),3≤x≤5} Verify conntinuity of g(x), for all x∈[0,5]
View SolutionLet f(x)=−x3+x2−x+1andg(x)={min(f(t)),0≤t≤xand0≤x≤1x−1,1<x≤2 Then, the value of limx→1g(g(x)), is........ .
View Solutionमाना f(x)=x3−x2+x+1 और g(x)={max{f(t),0≤t≤x}0≤x≤13−x1<x≤2
फलन g(x) की सततता तथा अवकलनीयता अंतराल (0, 2) पर ज्ञात कीजिए |
View SolutionLet f(x)=f1(x)−2f2(x), where ,where f1(x)={(min{x2,|x|}|x|≤1max{x2,|x|}|x|≤1) and f2(x)={(min{x2,|x|}|x|<1{x2,|x|}|x|≤1) and let g(x)={(min{f(t):−3≤t≤x,−3≤x≤0}max{f(t):0≤t≤x,0≤x≤3}) for −3≤x≤−1 the range of g(x) is
View SolutionLet f(x)=x3−x2+x+1 g(x) = max I {f(t),0≤t≤x},0≤x≤1=3−x,1<x≤2
Then in [0, 2] the points where g(x) is not differentiable is………
View SolutionLet f(x)=x3−x2+x+1 g(x)={max(f(t)),0≤t≤x},0≤x≤1}{3−x,1<x≤2}
Then in [0, 2] the points where g(x) is not differentiable is………
View SolutionLet f(x)=x3−x2+x+1andg(x)={maxf(t),0≤t≤xfor0≤x≤13−x,1<x≤2 Then, g(x) in [0, 2] is
View SolutionLet f(x)=1+4x−x2,∀x∈R g(x)=max{f(t),x≤t≤(x+1),0≤x<3min{(x+3),3≤x≤5} Verify conntinuity of g(x), for all x∈[0,5]
View Solution
