Some portion of a 20 meters long tree is broken by the wind and its top struck the ground at an angle of 30∘.Find the height of the point where the tree is broken. Solution in Bengali
Let AD be the tree before it was broken . AD= 20 m
Tree is broken at point B and the broken portion is touching the ground at point C. In triangle BAC,
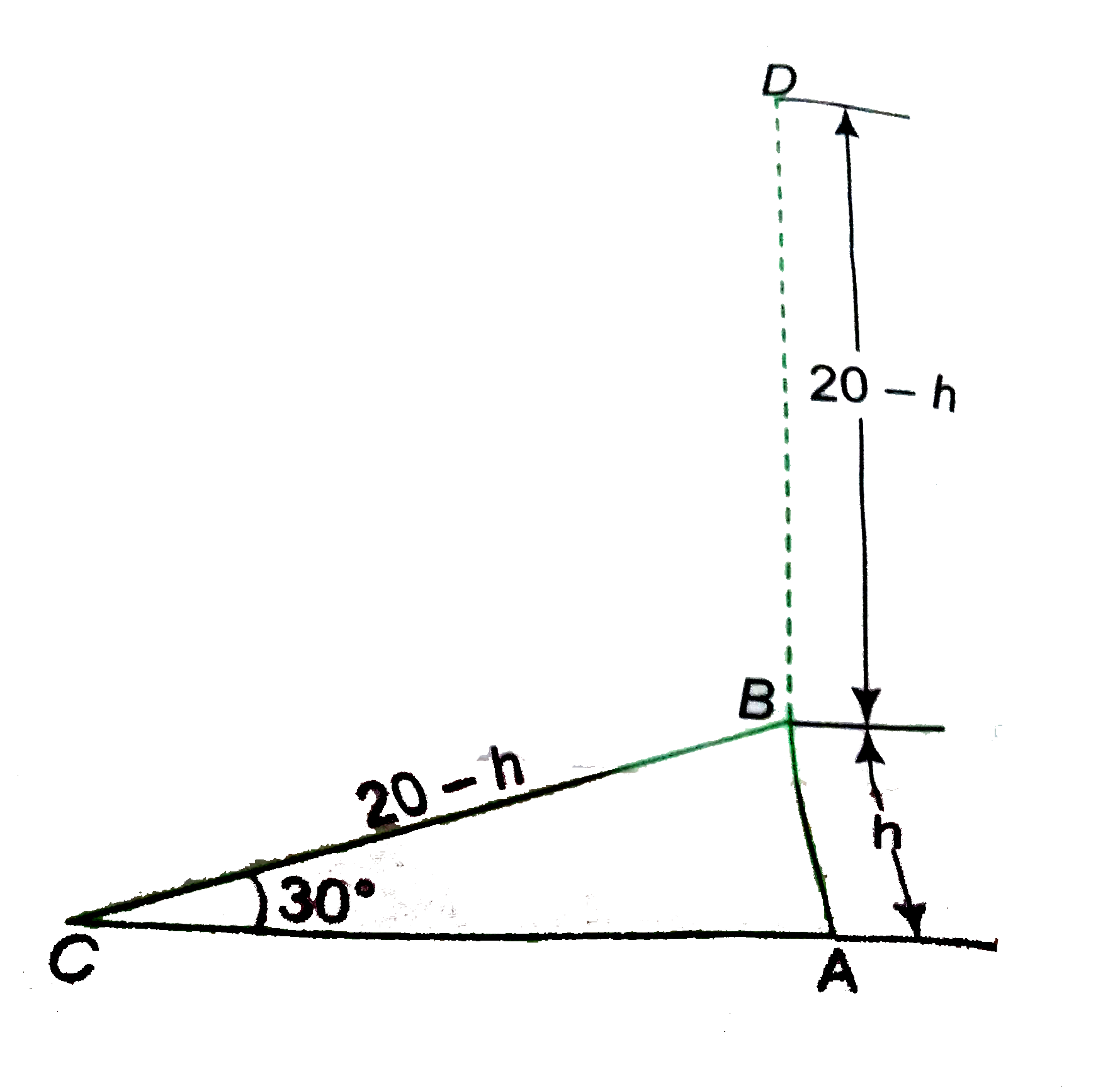
sin30∘=h20−h
⇒12=h20−h
⇒20−h=2h
⇒h=203m
Topper's Solved these Questions
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Exercises
18 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- HYPERBOLABOOK - CENGAGE PUBLICATIONCHAPTER - HYPERBOLAEXERCISE - COMPREHENSION TYPE
2 Videos
Similar Questions
The tops of two poles of height 20 m and 14 m are connected by a wire. If the wire makes an angle of 30o with horizontal, then the length of the wire is (a) 12 m (b) 10 m (c) 8 m (d) 6 m
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionThe circle x2+y2−8x=0 and hyperbola x29−y24=1 I intersect at the points A and B. Equation of a common tangent with positive slope to the circle as well as to the hyperbola is (A) 2x−√5y−20=0 (B) 2x−√5y+4=0 (C) 3x−4y+8=0 (D) 4x−3y+4=0
View SolutionA tree is broken by the wind. The top struck the ground at an angle of 30∘ and at a distance of 4 m from the root. Find the height of the tree before broken.
View SolutionThe upper part of a tree broken over by the wind makes an angle of 60∘ with the ground and the horizontal distance from the foot of the tree to the point where the top of the tree meets the ground is 10 metres. Find the height of the tree before broken.
View SolutionSome portion of a 20 meters long tree is broken by the wind and its top struck the ground at an angle of 30∘.Find the height of the point where the tree is broken.
View Solutionऑधी आने पर एक पेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखर जमीन को छूने लगता है और इसके साथ 60∘ का कोण बनाता है । पेड़ के पाद-बिन्दु को दूरी, जहाँ पेड़ का शिखर जमीन को छूता है, 3 m है । पेड़ की ऊँचाई ज्ञात कीजिए ।
View Solutionएक पेड़ हवा से टूट जाता है और इसका शिखर, जमीन पर इसकी जड़ से 30 मी.की दूरी पर 30∘के कोण से छूटा है | पेड़ की संम्पूर्ण ऊँचाई ज्ञात करें |
View SolutionA portion of a 30 m long tree is broken by tornado and the top struck up the ground making an angle 30∘ with ground level. The height of the point where the tree is broken is equal to :
View Solutionआँधी आने से एकपेड़ टूट जाता है और टूटा हुआ भाग इस तरह मुड़ जाता है कि पेड़ का शिखरजमीन को छूने लगता है और इसके साथ 30∘ का कोण बनाता है। पेड़ के पाद-बिंदु की दूरी, जहाँ पेड़ का शिखरजमीन को छूता है, 8m है। पेड़ की ऊँचाई ज्ञात कीजिए।
View SolutionA tree is broken by the wind. If the top of the tree struck the ground at an angle of 30∘ and at a distance of 30 m from the root, then the height of the tree is
View SolutionA portion of a 24 m high tree is broken by tornado and struck the ground making an angle of 30∘ with the ground. The height of the point where the tree is broken is equal to ___________ m
View SolutionSome portion of a 20 meters long tree is broken by the wind and its top struck the ground at an angle of 30∘.Find the height of the point where the tree is broken.
View Solutionएक वृक्ष का ऊपरी शीर्ष हवा से टूटकर भूमि से 30∘ का कोण बनाता है । वृक्ष की जड़ (Root) से उस बिंदु की दूरी 5 मी. है जहाँ शीर्ष भूमि को स्पर्श करता है । वृक्ष की ऊँचाई ज्ञात कीजिए।
View Solutionsome portion of a 30m long tree is broken by tornado and the top struck up the ground making an angle 30∘ with ground level. The height of the point where the tree is broken is equal to:
View Solution
