Solve : 2cos2θ+sinθ≤2, where π2≤θ≤3π2.Solution in Bengali
2cos2θ+sinθ≤2
⇒ 2(1−sin2θ)+sinθ≤2
⇒ −2sin2θ+sinθ≤0
⇒ 2sin2θ−sinθ≥0
⇒ sinθ(2sinθ−1)≥0
⇒ sinθ(sinθ−1/2)≥0,
which is possible if sinθ≤0 or sinθ≥1/2
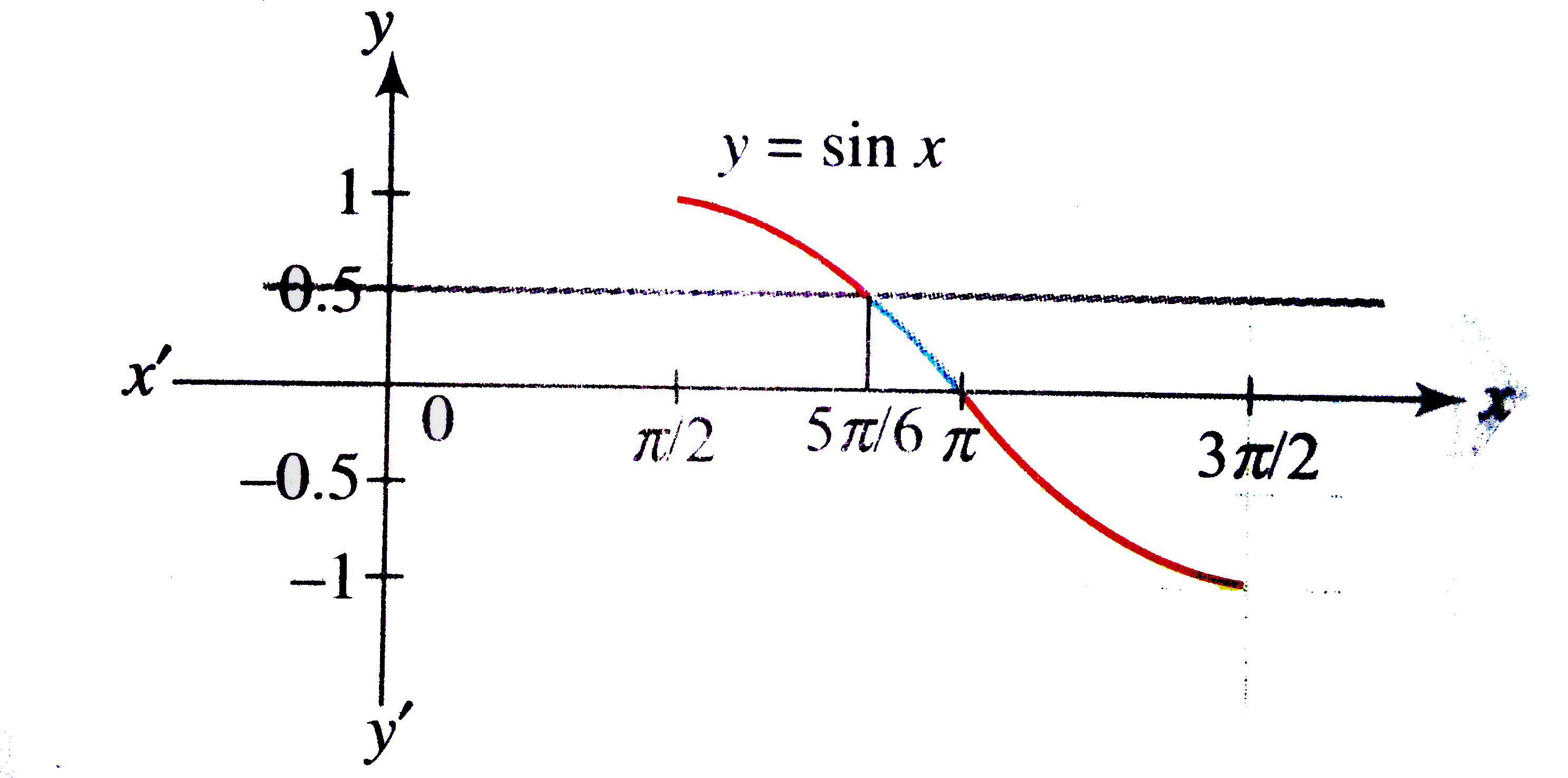
Now sinθ≥1/2⇒π/2≤θ≤5π/6 (from the figure)
And sinθ≤0⇒π≤θ≤3π/2 (from the figure)
Hence the required values of θ are given by θ∈[π/2,5π/6]∪[π,3π/2]
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - EXERCISES
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGE PUBLICATIONCHAPTER - HIGHT AND DISTANCE EXERCISE - Archives
3 Videos
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionDraw the graph of y=1(1/x).
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionSolve sin2θ−cosθ=14 for θ and write the value of theta in the interval 0≤θ≤2π
View SolutionifA=(θ:2cos2θ+sinθ≤2) and
b={θ:π2≤θ≤3π2}, then A∩B is equal to
View SolutionA={θ∣2cos2θ+sinθ≤2)}
B={θ∣∣∣π2≤θ≤3π2∣∣∣}: Find A∩B.
View SolutionSolve :
cosθcos2θcos3θ=14(0≤θ≤π)
View SolutionIf 2 sin ^(2) theta = 3 cos theta , where 0 le theta le 2 pi If so theta The value of
View Solution-sin^(8)theta le sin^(6)theat le sin^(4)theta le sin^(2)theta le 1 And …………. cos^(8)theta le cos^(6) theta le cos^(4)theta le cos^(2)theta le 1
View Solutionयदि 2sin2θ=3cosθ है जहाँ 0≤θ≤2π हैं तो θ मान ज्ञात कीजिए।
View Solutionif A=( theta :2 cos^(2)theta + sin theta le 2)and B= {theta :(pi)/(2) le theta le (3pi)/(2)} then A n B is equal to
View Solutionयदि A={θ:2cos2θ+sinθ≤2} तथा B={θ.π2≤θ≤3π2} है , तब बराबर है -
View SolutionSolve cosθ⋅cos2θ⋅cos3θ=14,0≤θ≤π
View SolutionSolve : 2cos2θ+sinθ≤2, where π2≤θ≤3π2.
View SolutionSolve cosθ⋅cos2θ⋅cos3θ=14,0≤θ≤π
View SolutionIf 2sin2θ=3cosθ,0≤θ≤2π,θ =
View Solution
