If lines x=y=zandx=y2=z3 and third line passing through (1,1,1) form a triangle of area √6 units, then the point of intersection of third line with the second line will be a. (1,2,3) b. 2,4,6 c. 43,63,123 d. none of theseSolution in Bengali
(1,2,3)
(2,4,6)
(43,83,123)
none of these
The correct Answer is:b
Let any point on the second line be (λ,2λ,3λ)
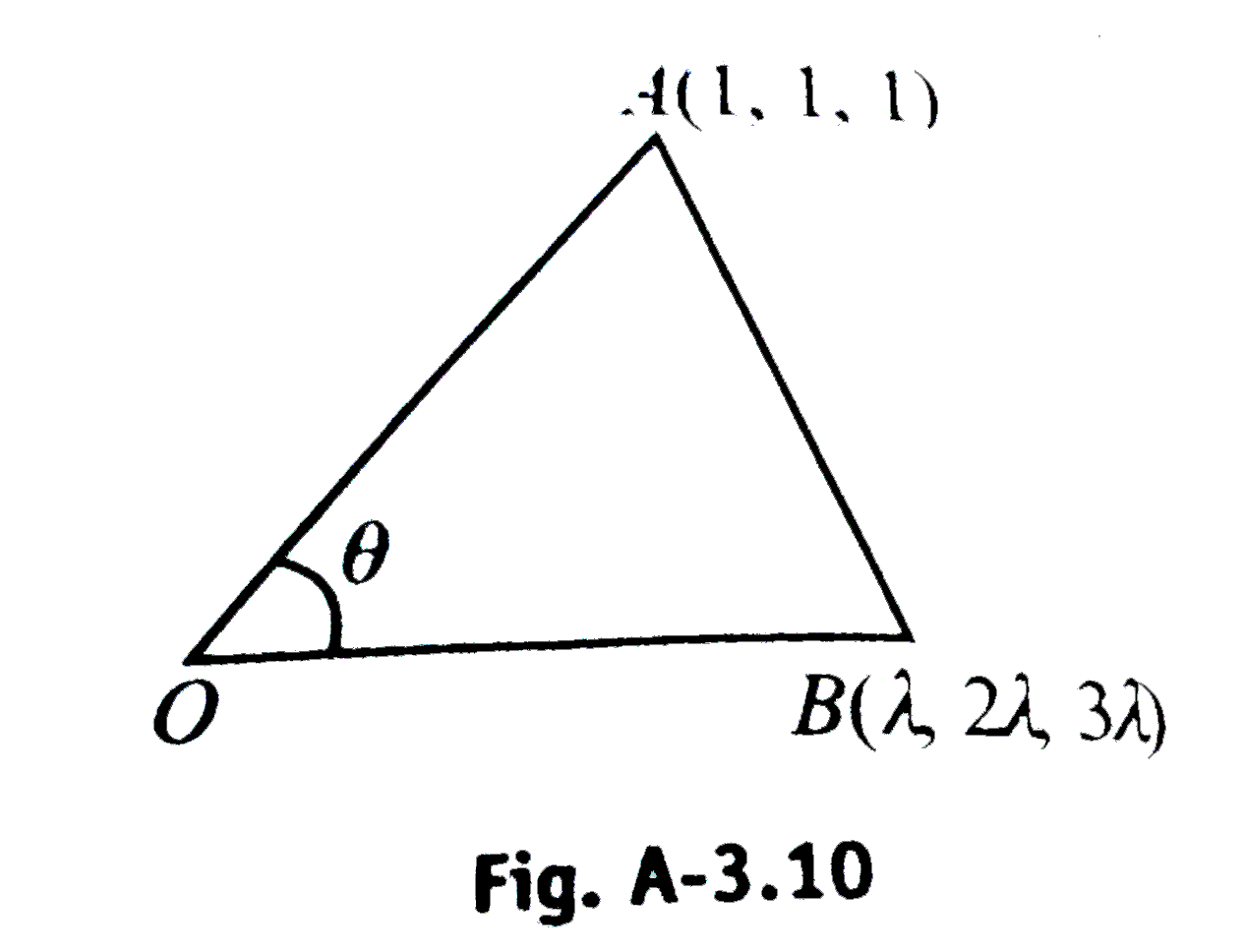
cosθ=6√42,sinθ=√6√42
ΔOAB=12(OA)OBsinθ
=12√3λ√14×√6√42=√6
or λ=2
So B is (2,4,6)
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CORRECT ANSWER TYPE
17 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - REASONING TYPE
10 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - SUBJECTIVE TYPE
17 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
291 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
Similar Questions
Let PM be the perpendicular from the point P(1,2,3) to the x−y plane. If →OP makes an angle θ with the positive direction of the z− axis and→OM makes an angle φ with the positive direction of x− axis, whereO is the origin and θandφ are acute angels, then a. cosθcosφ=1/√14 b. sinθsinφ=2/√14 c. tanφ=2 d. tanθ=√5/3
View SolutionStatement 1: Lines →r=ˆi+ˆj−ˆk+λ(3ˆi−ˆj)and→r=4ˆi−ˆk+μ(2ˆi+3ˆk) intersect. Statement 2: →b×→d=0 , then lines →r=→a+λ→band→r=→c+λ→d do not intersect.
View SolutionIf the direction cosines of a variable line in two adjacent points be l,m,nandl+δl,m+δm,n+δn the small angle δθas between the two positions is given by
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionFind the equation of a line which passes through the point (1,1,1) and intersects the lines x−12=y−23=z−34andx+21=y−32=z+14.
View SolutionIf lines x=y=zandx=y2=z3 and third line passing through (1,1,1) form a triangle of area √6 units, then the point of intersection of third line with the second line will be a. (1,2,3) b. 2,4,6 c. 43,63,123 d. none of these
View SolutionThe area of the triangle formed by the line x=3, y=4 and x=y is (a) sq. unit (b) 1 sq. unit (c) 2 sq. unit (d) None of these
View SolutionA line passing through the point (1,1,1) from a tiangle of area √6 sq. unit with the lines x=y=z and x=y2=z3. If the point of intersection of the line with the second line be (λ,2λ,3λ), then the value of λ is -
View SolutionA triangle is formed by Y-axis, the straight line L passing through the points (3,0)(1,43) and the straight line perpendicular to the line L and passing through the point (8,1). Then, the area of the triangle (in sq units) is
View SolutionA straight line through the point (2, 2) intersects the lines √3x+y=0 and √3x−y=0 at the points A and B. The equation to the line AB so that the triangle OAB is equilateral is
View SolutionA st. line through the point (2, 2) intersects the lines √3x+y=0and√3x−y=0 at the points A and B. The equation to the line AB so that the triangle OAB is equilateral is :
View SolutionFind the equation of the line passing through the point (−1,2,3) and perpendicular to the lines x2=y−1−3=z+2−2andx+3−1=y+32=z−13.
View SolutionIf lines x=y=zandx=y2=z3 and third line passing through (1,1,1) form a triangle of area √6 units, then the point of intersection of third line with the second line will be a. (1,2,3) b. 2,4,6 c. 43,63,123 d. none of these
View SolutionIf lines x=y=zandx=y2=z3 and third line passing through (1,1,1) form a triangle of area √6 units, then the point of intersection of third line with the second line will be a. (1,2,3) b. 2,4,6 c. 43,63,123 d. none of these
View SolutionIf lines x=y=zandx=y2=z3 and third line passing through (1,1,1) form a triangle of area √6 units, then the point of intersection of third line with the second line will be a. (1,2,3) b. 2,4,6 c. 43,63,123 d. none of these
View Solution
