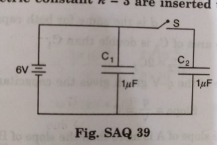
Figure shows two identical capacitors C1 and C2 each of 1μF capacitance connected to a battery of 6 V. initially switch S is closed. After sometime S is left open and dielectric slab of dielectric constant k = 3 are inserted to fill completely the space between the plates of the two capacitors. How will the potential difference between the plates of the capacitors be affected after the slabs are inserted?
 Solution in Punjabi
Solution in Punjabi
Step by step video & image solution for Figure shows two identical capacitors C_1 and C_2 each of 1 mu F capacitance connected to a battery of 6 V. initially switch S is closed. After sometime S is left open and dielectric slab of dielectric constant k = 3 are inserted to fill completely the space between the plates of the two capacitors. How will the potential difference between the plates of the capacitors be affected after the slabs are inserted? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Similar Questions
Two identical parallel plate capacitors A and B are connected to a battery of V volts with the switch S closed . The switch is now opened and the free space between the plates of the capacitors is filled with dielectric of dielectric constant K . Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric .
View SolutionFig, shows two indentical capacitors C_(1) and C_(2) each of 1 uF capacitance connected to a battery of 6V. Initially, swich S is closed. After some time, the swich S is left open and dielectric slabs of K = 3 are inserted to filll completely the space between the plates of two capacitors . How will (i) the charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted ?
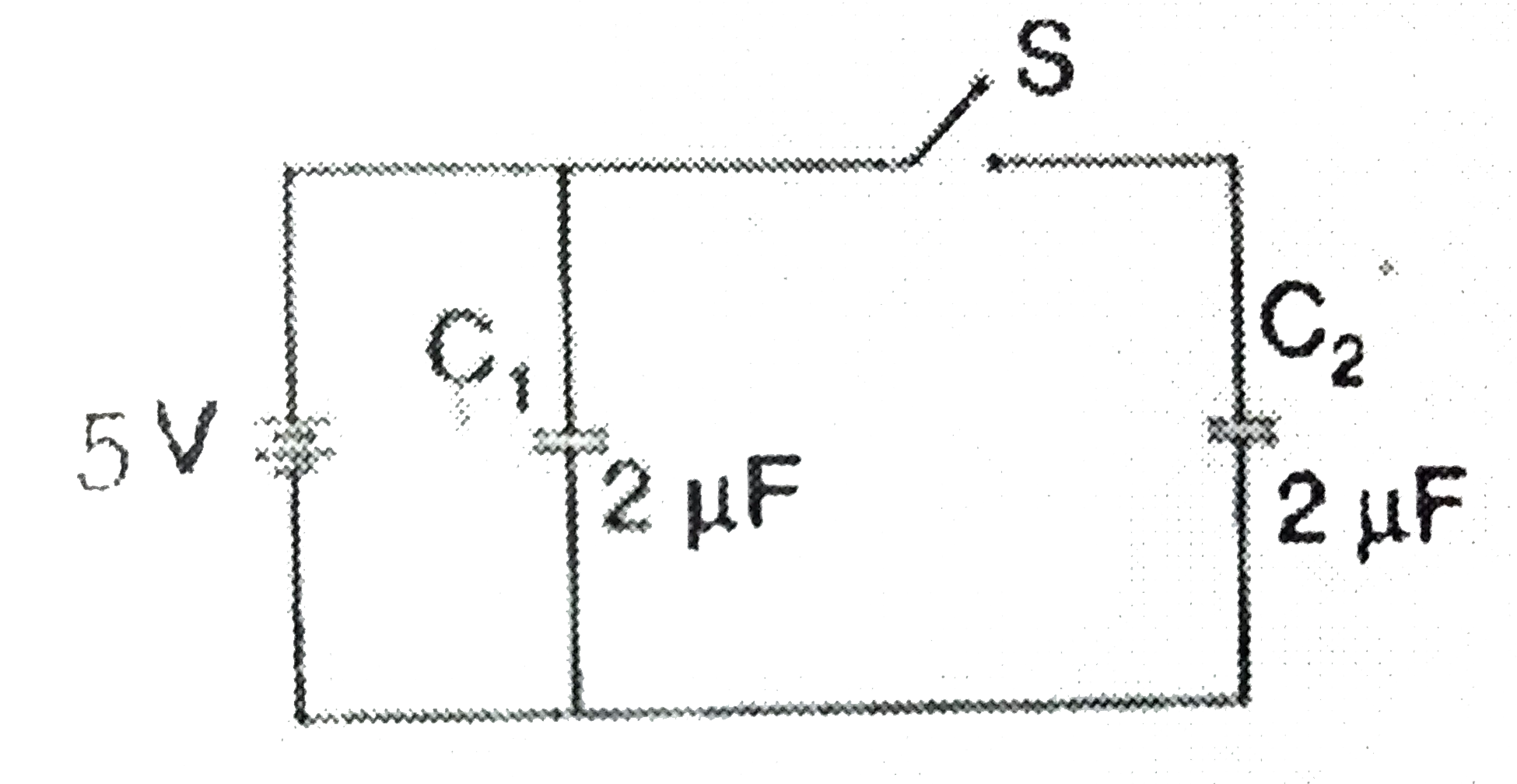
03:16View SolutionFigure shows two identical capacitors C1andC2 each of 2μF capacitance, connected to a battery of 5 V. Initially switch 'S' is closed. After some time 'S' is left open and dielectric slavs of dielectric constant K = 5 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted?
 06:46View Solution
06:46View SolutionFigure shows two identical caoacitors C_1 and C_2 each of 1.5muF caoacitance, connected to a battery of 2 V. Initially switch 'S' is closed. After some time 's' is left open and dielectric slabs of dielectric constant K=2 are inserted to fill completely the space between the plates of the two capacitors. How will the (i) charge and (ii) potential difference between the plates of the capacitors be affected after the slabs are inserted.
04:32View SolutionThe figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant(or relative permittivity) 3. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
 05:05View Solution
05:05View SolutionFig. shows two identical parallel plate capacitors connected to a battery with the switch .S. closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of K = 3. Find the ratio of the total electrostatic energy stored in both the capacitors before and after the introduction of the slab.
View SolutionThe figure shows two identical parallel plate capacitors connected to a battery with the switch S closed. The switch is now opened and the free space between the plates of the capacitors is filled with a dielectric of dielectric constant(or relative permittivity) 3. Find the ratio of the total electrostatic energy stored in both capacitors before and after the introduction of the dielectric.
05:05View SolutionTwo identical parallel plate capacitors are connected in series and then joined in series with a battery of 100V. A slab of dielectric constant K=3 is inserted between the plates of the first capacitor. Then, the potential difference across the capacitor will be, respectively.
02:04View Solution

