आरम्भिक वेग $v = v_{0} \hat{i} (v_{0} > 0)$ और द्रव्यमान m का कोई इलेक्ट्रॉन किसी विद्युत क्षेत्र $E = - E_{0} \hat{i} (E_{0} =$ स्थिरांक $> 0)$ में t = 0 पर प्रवेश करता है। यदि प्रारम्भ में इस इलेक्ट्रॉन की दे-ब्रॉग्ली तरंगदैर्ध्य $λ_{0}$ है, तो समय t पर इसकी दे-ब्रॉग्ली तरंगदैर्ध्य होगी

A

$λ_{0} t$

B

$λ_{0} (1 + \frac{e E_{0}}{m v_{0}} \cdot t)$

C

$\frac{λ_{0}}{(1 + \frac{e E_{0}}{m v_{0}} \cdot t)}$

D

$λ_{0}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

प्रश्नानुसार,
$v = v_{0} \hat{i}, E = - E_{0} \hat{i}$

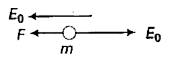
अत: विद्युत क्षेत्र के कारण इलेक्ट्रॉन पर बल का परिमाण,
$| F | = q | E |$
$\Rightarrow F = e E_{0}$
न्यूटन के गति के द्वितीय नियम द्वारा,
F = ma
$∴ F = m a = e E_{0}$
$\Rightarrow a = \frac{e E_{0}}{m} ... (i)$
या $a = \frac{(- e) (- E_{0} \hat{i})}{m} = \frac{e E_{0}}{m} \hat{i}$
गति के प्रथम समीकरण द्वारा, $v = u + a t$
यहाँ, u (प्रारम्भिक वेग) $= v_{0}$
$v = v_{0} + \frac{e E_{0} t}{m}$ [समी (i) से] ...(ii)
इलेक्ट्रॉन को प्रारम्भिक दे-ब्रोग्ली तरंगदैर्ध्य,
$λ_{0} = \frac{h}{m v_{0}} \Rightarrow h = λ m v_{0} ... (i i i)$
t समय पश्चात्, दे-ब्रोग्ली तरंगदैर्ध्य,
$λ = \frac{h}{m v}$
समी (ii) से v का मान रखने पर
$λ = \frac{h}{m (v_{0} + \frac{e E_{0}}{m} t)} = \frac{h}{m v_{0} [1 + \frac{e E_{0}}{m v_{0}} t]}$
$= \frac{λ m v_{0}}{m v_{0} [1 + \frac{e E_{0}}{m v_{0}} t]}$ [समी (iii) से]
$= \frac{λ_{0}}{[1 + \frac{e E_{0}}{m v_{0}} t]} ∴ λ = \frac{λ_{0}}{1 + \frac{e E_{0}}{m v_{0}} t}$

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

Similar Questions

NEET PREVIOUS YEAR-NEET सॉल्वड पेपर 2018 -भौतिकी

Home
Ask Doubt
Profile