Repeat Qestiobn 6,if ¯¯¯AB happens to be a diameter.Solution in Punjabi
Step by step video & image solution for Repeat Qestiobn 6,if bar AB happens to be a diameter. by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Draw a circle of radius 4 cm.
View SolutionWrite all the factors of the following number :
12
View SolutionThere are 45 persons working in an office.If the number of females is 25 and the remaining are males,find the ratio of :
the number of females to number of males.
View SolutionABC is an equilateral triangle of side ‘a'. Then bar(AB).bar(BC) +bar(BC).bar(CA)+ bar(CA).bar(AB) =
View SolutionProve the following boolean relations.
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯A+AB+¯¯¯¯¯¯AB=0
View Solution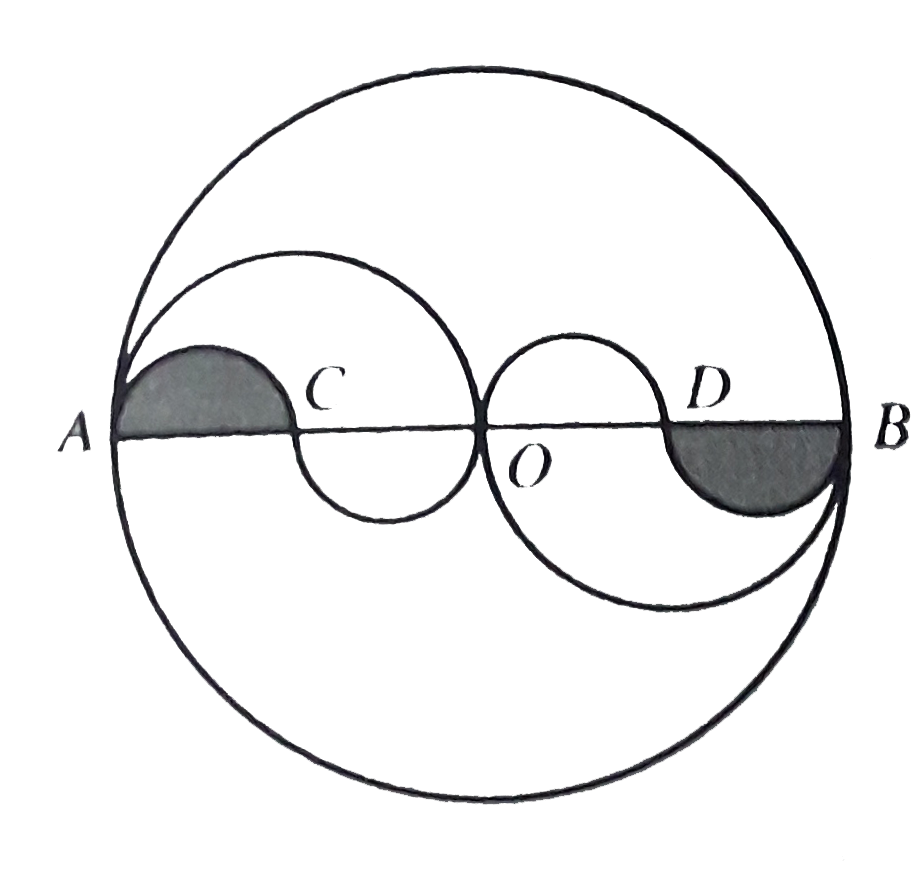
In the circle shown above, O is the center and ¯¯¯¯¯¯AB is a diameter . There are two semicircles with diameters ¯¯¯¯¯¯AO and ¯¯¯¯¯¯BO , and four smaller semicircles with congruent diameters ¯¯¯¯¯¯AC,¯¯¯¯¯¯CO,¯¯¯¯¯¯OD and ¯¯¯¯¯¯DB . A point is picked at random in the large circle . What is the probability that it lands in a shaded region ?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
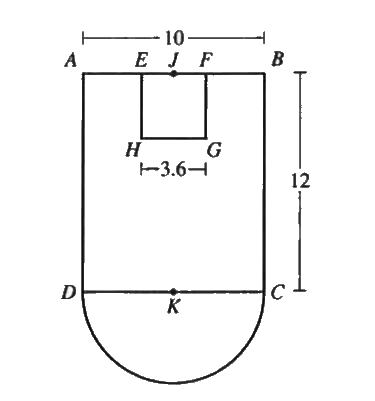
What is the length, in meters, of ¯¯¯¯¯¯JD?
View SolutionIn the figure below, ABCD is a rectangle, EFGH is a square, and ¯¯¯¯¯¯CD is a diameter of a semicircle. Point K is the midpoint of ¯¯¯¯¯¯CD. Point J is the midpoint of both ¯¯¯¯¯¯AB and ¯¯¯¯¯¯EF. Points E and F lie on ¯¯¯¯¯¯AB. The 3 given lengths are in meters.
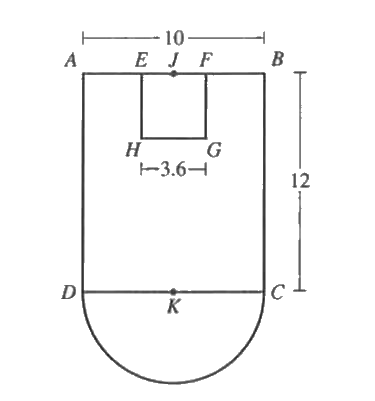
What is the length, in meters, of are ¯¯¯¯¯¯CD?
View SolutionIf (1, 2), (4, 3), (6, 4) are the midpoints of the sides ¯¯¯¯¯¯BC,¯¯¯¯¯¯CA,¯¯¯¯¯¯AB of ΔABC, then the equation of AB is
View SolutionIn figure, ¯¯¯¯¯¯AB is a diameter of the circle, ¯¯¯¯¯¯CD is a chord equal to the radius of the circle. ¯¯¯¯¯¯AC and ¯¯¯¯¯¯BD when extended intersect at a point E. Prove that ∠AEB=6∘.
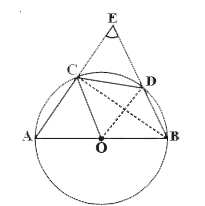
View Solution6 ডেসিমি. দৈর্ঘ্যর ব্যাসের একটি নিরেট রৌপ্য গোলোক গলিয়ে 1 ডেসিমি. লম্বা একটি লম্ব বৃত্তাকার দণ্ড তৈরি করা হলে, দণ্ডটির ব্যাসের দৈর্ঘ্য হিসাব করো।
View SolutionAB+¯¯¯¯¯¯AB is always
View SolutionA point I is the centre of a circle inscribed in a triangle ABC then show that
∣∣¯¯¯¯¯¯BC∣∣¯¯¯¯¯IA+∣∣¯¯¯¯¯¯CA∣∣¯¯¯¯¯IB+∣∣¯¯¯¯¯¯AB∣∣¯¯¯¯¯IC=¯0
View SolutionIf I is the centre of a circle inscribed in a ΔABC, then ∣∣¯¯¯¯¯¯BC∣∣¯¯¯¯¯IA+∣∣¯¯¯¯¯¯CA∣∣¯¯¯¯¯IB+∣∣¯¯¯¯¯¯AB∣∣¯¯¯¯¯IC=
View SolutionABC is an equitateral triangle of side 'a'. Then ¯¯¯¯¯¯AB.¯¯¯¯¯¯BC+¯¯¯¯¯¯BC.¯¯¯¯¯¯CA+¯¯¯¯¯¯CA.¯¯¯¯¯¯AB=
View Solution
