Let P be the point on parabola y2=4x which is at the shortest distance from the center S of the circle x2+y2−4x−16y+64=0 let Q be the point on the circle dividing the line segment SP internally. ThenSolution in Tamil
SP=2√5
SQ:QP(√5+1):2
the x-intercept of the normal to the parabola at P is 6
the slope of the tangent to the circle at Q is 12
The correct Answer is:A, C, D
Tangent to y2=4x at (t2,2t) is
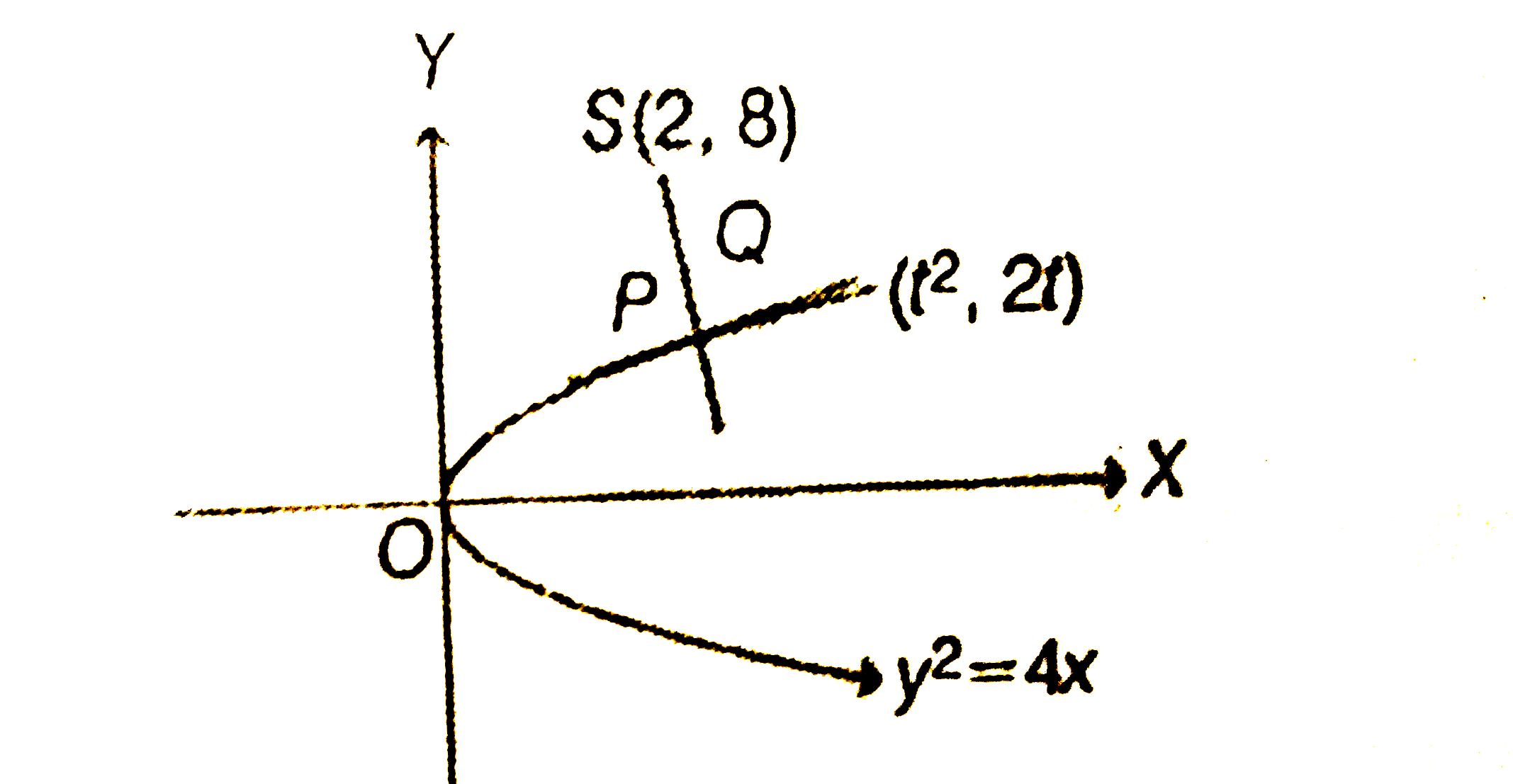
y(2t)=2(x+t2)
⇒yt=x+t2
Equation of normal of P(t2,2t) is
y+tx=2t+t3
Since, normal at P passes through centre of circle S(2,8).
∴8+2t+t3
⇒t=2, i., P (4,4)
[Since, shortest distance between two curves lie along their common normal and the common normal will pass through the centre of circle]
∴SP=√(4−2)2+(4−8)2=2√5
∴ Opion (a) is correct.
Also, SQ=2
∴PQ=SP−SQ=2√5−2
Thus, SQQP=1√5−1=√5+14
∴ Option (b) is wrong
Now x intercept of normal is x=2+22=6
∴ Option (c ) is corect
Slope of tangent =1t=12
∴ Option (d) is correct.
Similar Questions
Let (x,y) be any point on the parabola y^2 = 4x . Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
View SolutionLet P be the point on parabola y2=4x which is at the shortest distance from the center S of the circle x2+y2−4x−16y+64=0 let Q be the point on the circle dividing the line segment SP internally. Then
View Solutionमाना (x,y) परवलय y2=4x पर स्थित कोई बिन्दु है। माना P वह बिन्दु है, जो कि बिन्दुओं (0, 0) तथा (x,y) को मिलाने वाले रेखाखण्ड को अनुपात 1 : 3 में विभाजित करता है, तो P का बिन्दुपथ है।
View Solutionमाना कि परवलय (parabola) y2=4x पर P एक ऐसा बिन्दु है जो वृत्त x2+y2−4x−16y+64=0 के केन्द्र बिन्दु S से न्यूनतम दूरी पर है | माना कि वृत्त पर बिन्दु Q ऐसा है कि वह रेखाखंड SP को आंतरिक विभाजित करता है | तब
View SolutionLet P be the point on the parabola y2=4x which is at the shortest distance from the center S of the circle x2+y2−4x−16y+64=0. Let Q be the point on the circle dividing the line segment SP internally. Then
View SolutionLet (x,y) be any point on the parabola y^2 = 4x . Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
View SolutionLet (x,y) be any point on the parabola y^2 = 4x . Let P be the point that divides the line segment from (0,0) and (x,y) n the ratio 1:3. Then the locus of P is :
View SolutionLet P be the point on parabola y2=4x which is at the shortest distance from the center S of the circle x2+y2−4x−16y+64=0 let Q be the point on the circle dividing the line segment SP internally. Then
View Solution
