Let $P (3, 2, 6)$ be a point in space and $Q$ be a point on line $\to r = (ˆ i - ˆ j + 2 ˆ k) + μ (- 3 ˆ i + ˆ j + 5 ˆ k) .$ Then the value of $μ$ for which the vector $\to P Q$ is parallel to the plane $x - 4 y + 3 z = 1$ is a. 1/4 b. -1/4 c. 1/8 d. -1/8Solution in Tamil

A

$\frac{1}{4}$

B

$- \frac{1}{4}$

C

$\frac{1}{8}$

D

$- \frac{1}{8}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Given, $O Q = (1 - 3 μ) ˆ i + (μ - 1) ˆ j + (5 μ + 2) ˆ k$
and $O P = 3 ˆ i + 2 ˆ j + 6 ˆ k [where, O is origin]$

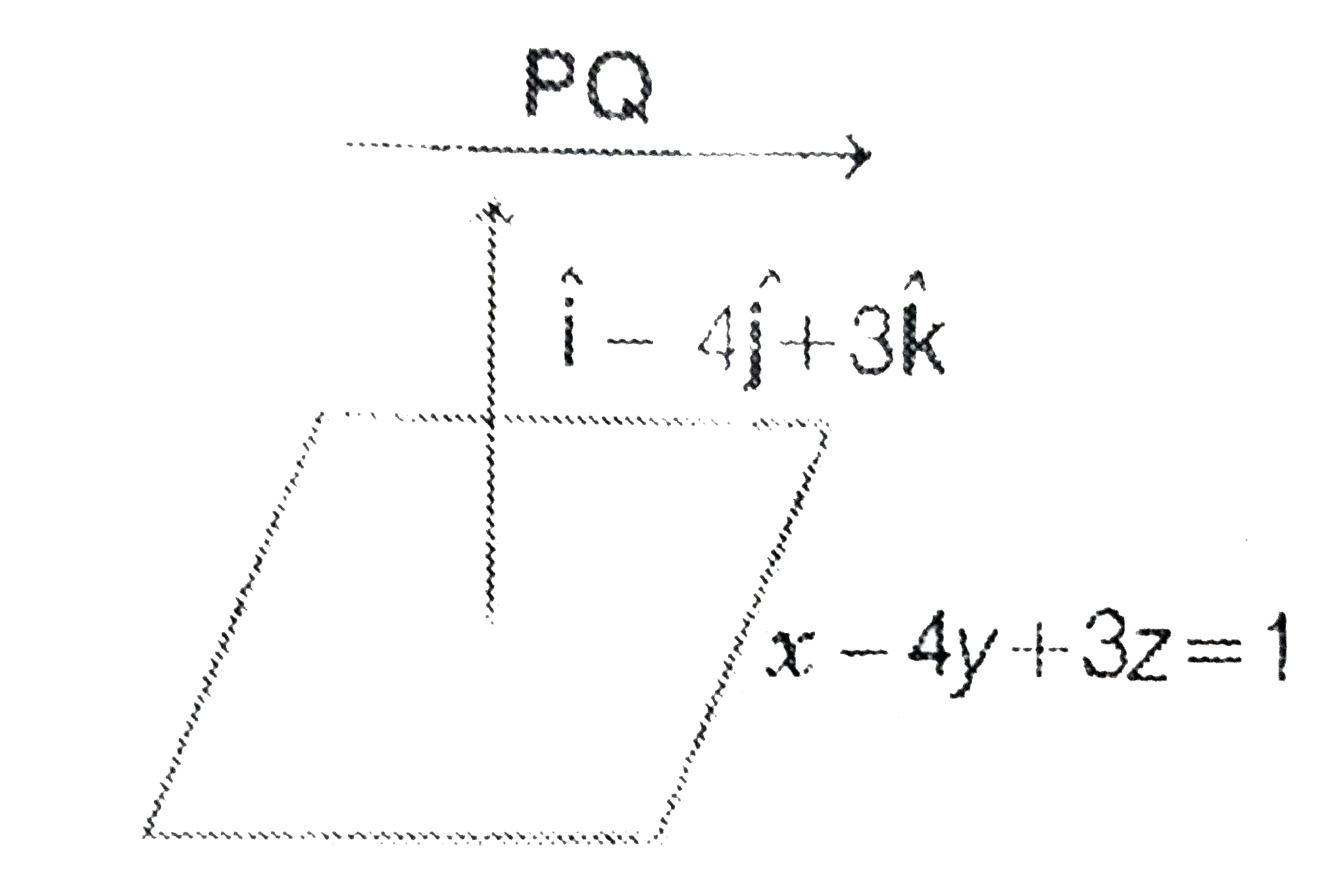
Now, $P Q = (1 - 3 μ - 3) ˆ i + (μ - 1 - 2) ˆ j + (5 μ + 2 - 6) ˆ k$
$= (- 2 - 3 μ) ˆ i + (μ - 3) ˆ j + (5 μ - 4) ˆ k$
$∵ PQ is parallel to the plane x - 4 y + 3 z = 1 .$
$∴ - 2 - 3 μ - 4 μ + 12 + 15 μ - 12 = 0$
$\Rightarrow 8 μ = 2 \Rightarrow μ = \frac{1}{4}$

Updated on:21/07/2023

|

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile