Consider the cube in the first octant with sides OP,OQ and OR of length 1, along the x-axis, y-axis and z-axis, respectively, where O(0,0,0) is the origin. Let S(12,12,12) be the centre of the cube and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If →p=−→SP,→q=−−→SQ,→r=−−→SR and →t=−→ST then the value of ∣∣(→p×→q)×(→r×(→t)∣isSolution in Tamil
The correct Answer is:(0.5)
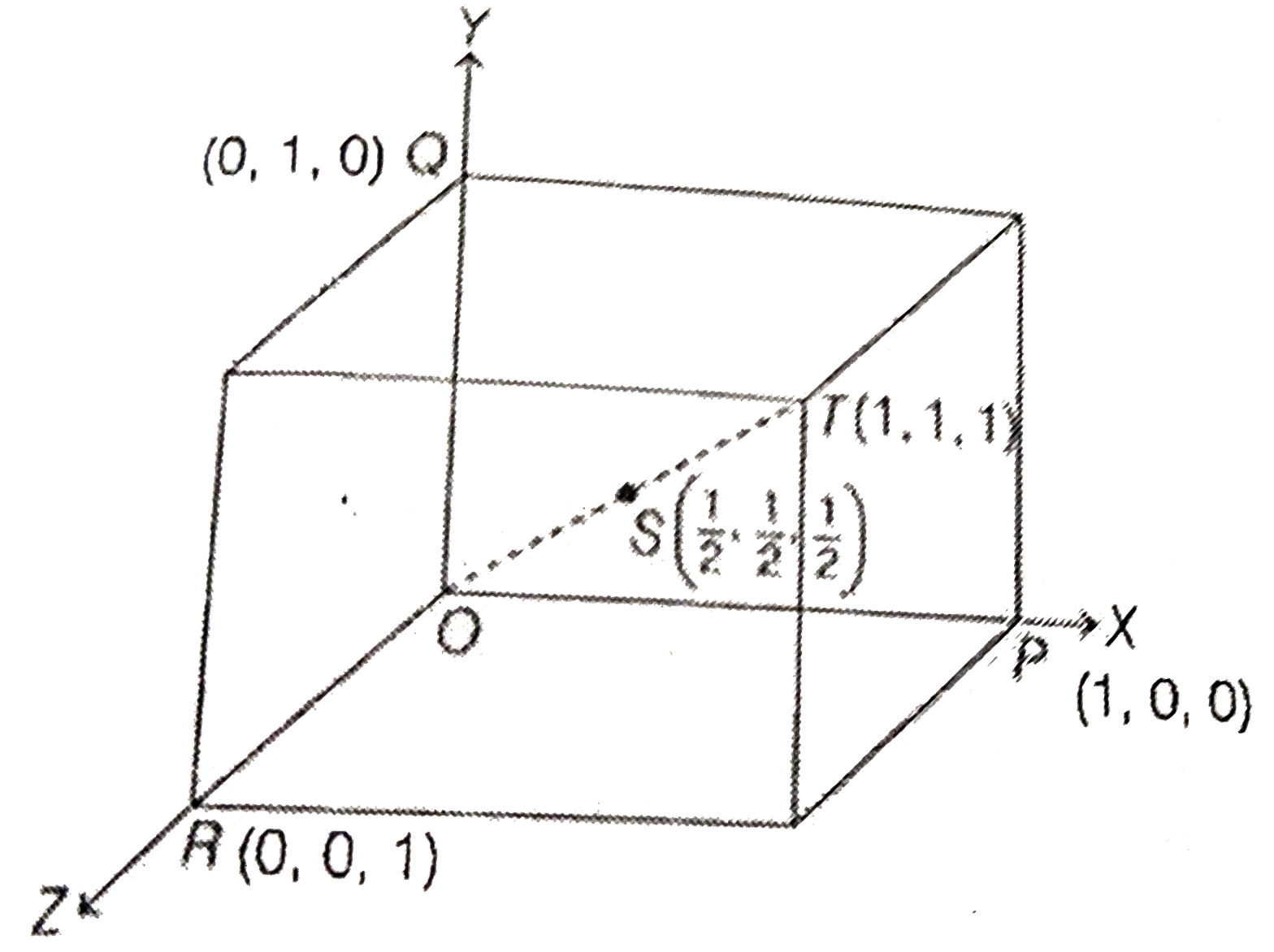
(0.5) Here P(1,0,0) Q(0,1,0) R (0,0,1) , T =(1,1,1) and
S=(12,12,12)
Now →P=−→SP=−−→OP−−−→OS
=(12ˆi−12ˆj−12ˆk)=12(ˆi−ˆj−ˆk)
→q=−−→SQ=12(ˆi+ˆj−ˆk)
→r=−−→SR=12(−ˆi−ˆj+ˆk)
And →t=−→ST=12(ˆi+ˆj+ˆk)
→p×→q=14∣∣
∣
∣∣ˆiˆjˆk1−1−1−11−1∣∣
∣
∣∣=14(2ˆi+2ˆj)
and→r×→t=14∣∣
∣
∣∣ˆiˆjˆk−1−11111∣∣
∣
∣∣=14(−2ˆi+2ˆj)
Now (→p×→q)×(→r×→t)=116∣∣
∣
∣∣ˆiˆjˆk222−220∣∣
∣
∣∣
=116(8ˆk)=12ˆk
∴(p×q)×(→r×→t)=∣∣∣12ˆk∣∣∣=12=0.5
Similar Questions
प्रथम अष्टांश में एक ऐसे घन पर विचार कीजिए, जिसकी भुजाओं OP, OQ और OR की लम्बाई 1 है और जो क्रमश: x-अक्ष, y-अक्ष और z-अक्ष के अनुदिश हैं, जहाँ O(0,0,0) मूलबिन्दु है | मना कि घन का केन्द्र S(12,12,12) है, शीर्ष T मूलबिन्दु O के सम्मुख वाला वह शीर्ष है कि बिन्दु S विकर्ण OT पर स्थित है | यदि →p=−→SP,→q=−−→SQ,→r=−−→SR और →t=−→ST, तब ∣∣(→p×→q)×(→r×→t)∣∣ का मान है
View SolutionIf →p=→a−→b,→q=→a+→b,|→a|=∣∣→b∣∣=t then |→p×→q|=
View SolutionConsider the cube in the first octant with sides OP,OQ and OR of length 1, along the x-axis, y-axis and z-axis, respectively, where O(0,0,0) is the origin. Let S(12,12,12) be the centre of the cube and T be the vertex of the cube opposite to the origin O such that S lies on the diagonal OT. If →p=−→SP,→q=−−→SQ,→r=−−→SR and →t=−→ST then the value of ∣∣(→p×→q)×(→r×(→t))∣∣is
View SolutionIF →p×→q=→r and →q×→r=→p then
View Solutionvec p , vec q ,a n d vec r are three mutually perpendicular vectors of the same magnitude. If vector vec x satisfies the equation vec pxx(( vec x- vec q)xx vec p)+ vec qxx(( vec x- vec r)xx vec q)+ vec rxx(( vec x- vec p)xx vec r)=0,t h e n vec x is given by a. 1/2( vec p+ vec q-2 vec r) b. 1/2( vec p+ vec q+ vec r)"" c. 1/3( vec p+ vec q+ vec r) d. 1/3(2 vec p+ vec q- vec r)
View SolutionLet vec(p),vec(q),vec(r) be three unit vectors such that vec(p)xxvec(q)=vec(r) . If vec(a) is any vector such that [vec(a),vec(q),vec(r )]=1,[vec(a),vec(r),vec(p )]=2 , and [vec(a),vec(p),vec(q )]=3 , then vec(a)=
View SolutionColumn- IColumn II(Operation of nonzero vectors→Pand→Q)(Possivle angle between→Pand→Q)(A)∣∣→P×→Q∣∣=0(P) 90∘(B)∣∣→P×→Q∣∣=√3→P.→Q(Q) 180∘(C)→P+→Q=→RandP+Q=R(R) 60∘(D)∣∣→P+→Q∣∣=∣∣→P−→Q∣∣(S) 0∘(T) 30∘
View SolutionLet vec(p),vec(q),vec(r) be three unit vectors such that vec(p)xxvec(q)=vec(r) . If vec(a) is any vector such that [vec(a)vec(q)vec(r )]=1,[vec(a)vec(r)vec(p )]=2 , and [vec(a)vec(p)vec(q )]=3 , then vec(a)=
View Solution
