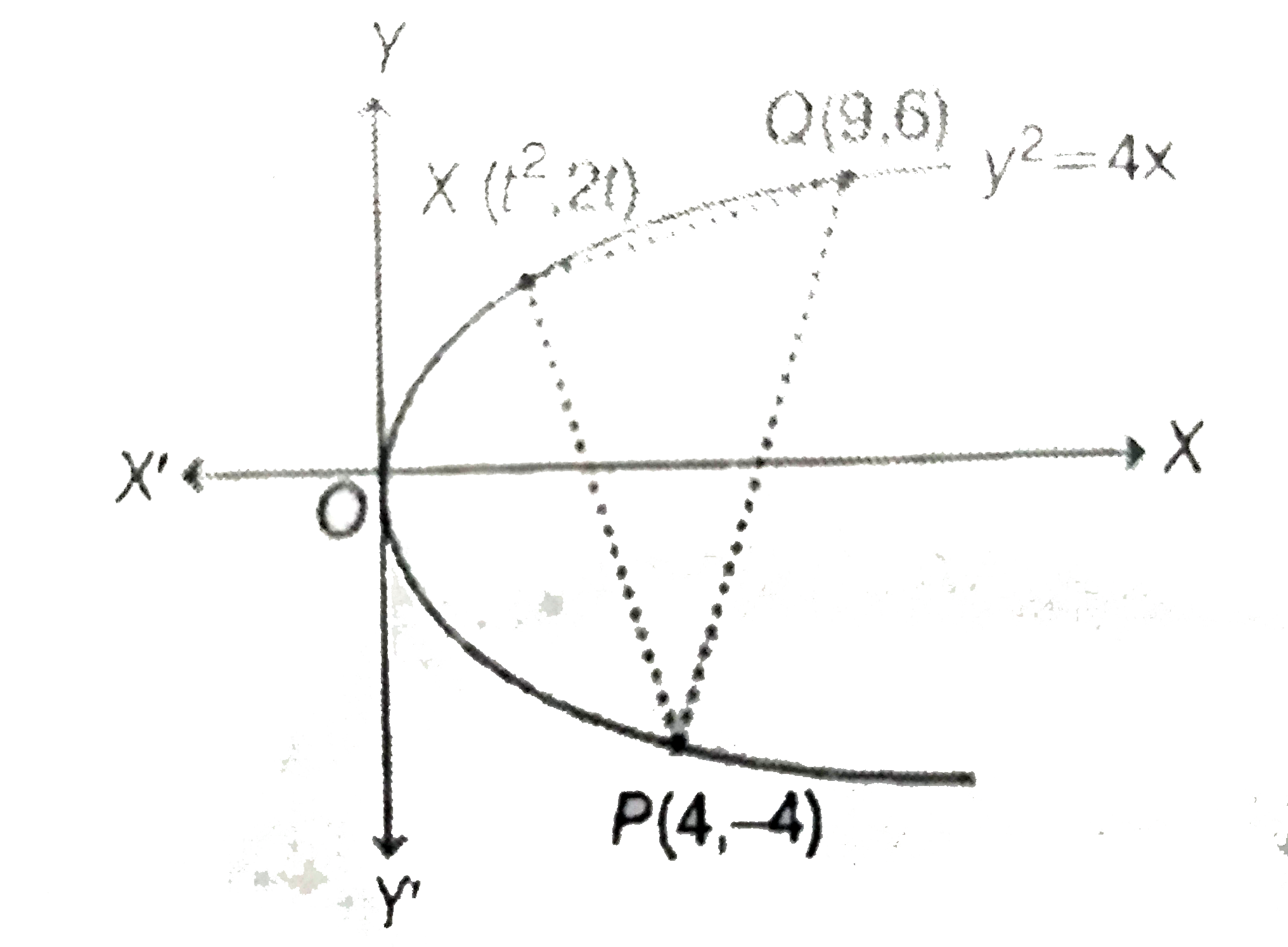
Consider the parabola y2=4x, let P and Q be two points (4,−4) and (9,6) on the parabola. Let R be a moving point on the arc of the parabola whose x-coordinate is between P and Q. If the maximum area of triangle PQR is K, then (4K)1/3 is equal to Solution in Tamil
1252
752
6254
1254
The correct Answer is:D
Given parabola is y2=4x,
Since, X lies on the parabola, so let the fcoordinates of X be (t2,2t). Thus the coordinates of the vertices of the traingle PXQ are P(4,4),x(t22t) and Q (9,6).
∴Area ofΔPXQ=12∣∣
∣
∣∣∣∣
∣
∣∣4−41t22t1961∣∣
∣
∣∣∣∣
∣
∣∣
=12∣∣[4(2t−6)+4(t29−)+1(6t2−18t)]∣∣
=12∣∣[8t−24+4t2−36+6t2−18t]∣∣
=∣∣5t2−5t−30∣∣=|5(t+2)(t−3)|
Now, as X is any point on the are POQ of the parabola, therefore ordinate of point X,2t∈(−4,6)⇒t∈(−2,3).
∴Area ofΔPXQ=−5(t+2)(t−3)=−5t2+5t+5t+30
[∵|x−a|=−(x−a).ifx<a]
The maximum area (in square units)
=−[25−4(−5)(30)−(−5)]=1254
[∵ Maximum value of quadratic expression ax2+bx+c,whena<0is−D4α]
Similar Questions
From the point (3 0) 3- normals are drawn to the parabola y2=4x. Feet of these normal are P ,Q ,R then area of triangle PQR is
View SolutionConsider the parabola y2=4x. Let P and Q be points on the parabola wher P(4,−4)andQ(9,6). Let R be a point on the area of the parabola between P and Q. Then the area of ΔPQR is largest when
View SolutionLet P,Q,R be three points on parabola y2=4x and normal P and R meet at Q, then the locus of the mid-points of the chord PR is a parabola whose vertex is at
View SolutionLet A(4,−4) and B(9,6) be points on the parabola y2=4x. Let C be chosen on the on the arc AOB of the parabola where O is the origin such that the area of ΔACB is maximum. Then the area (in sq. units) of ΔACB is :
View SolutionLet A (4, -4) and B (9,6) be a parabola. y^2=4x There are two points on if a point C on the arc AOB of the parabola (where O is the origin point) is chosen such that triangleACB If the area is maximum triangleACB The area of (in square units) is
View SolutionLet P(4,−4) and Q(9,6) be two points on the parabola, y2=4x and let X be any point on the are POQ of this parabola, where O is the vertex of this parabola, such that the area of ΔPXQ is maximum. Then this maximum area (in square units) is 25k4. The value of k is
View SolutionLet A(4,−4) and B(9,6) be points on the parabola y2=4x. Let C be chosen on the on the arc AOB of the parabola where O is the origin such that the area of ΔACB is maximum. Then the area (in sq. units) of ΔACB is :
View Solution
