ABCD is a tetrahedron such that each of the △ABC, △ABD and △ACD has a right angle at A. If ar(△ABC)=k1.Ar(△ABD)=k2,ar(△BCD)=k3 then ar(△ACD) is Solution in Tamil
√k21+k22+k23
√k1k2k3k1+k2+k3
√∣∣k21+k22−k23∣∣
√∣∣k22−k21−k23∣∣
The correct Answer is:C
Let us suppose that A is origin .
ar(△ABC)2+ar(△ACD)2+ar(△ABD)2=ar(△BCD)2
⇒ar(△ACD)=√∣∣k21+k22−k23∣∣
Topper's Solved these Questions
Similar Questions
The shortest distance between line y-x=1 and curve x=y2 is
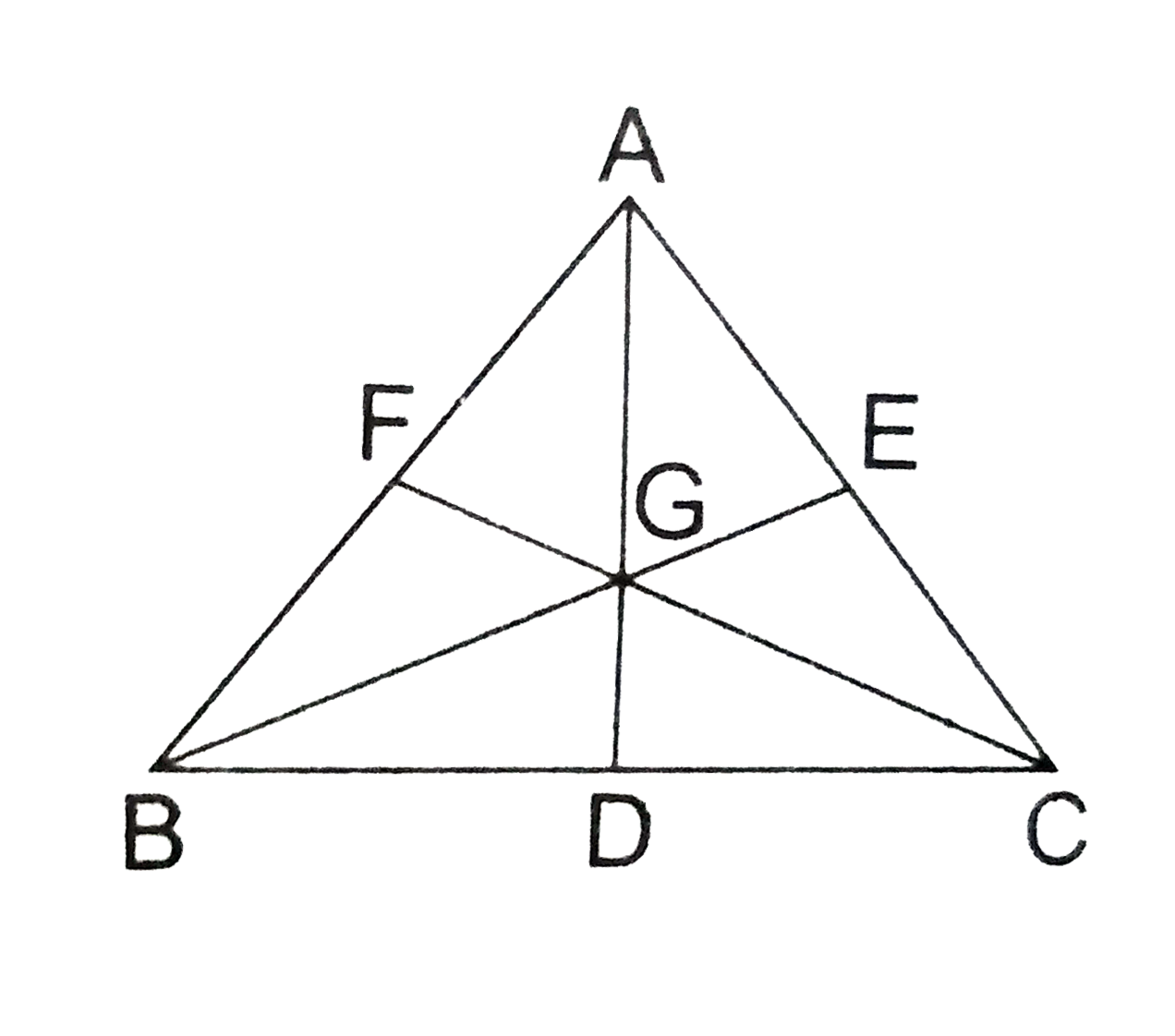
View SolutionIf the medians of a △ABC intersect at G, show that
ar(△AGB)=ar(△AGC)=ar(△BGC)
=13ar(△ABC).
View SolutionIn the adjoining figure, ABC and BDE are two equilateral triangle such that D is the midpoint of BC. If AE intersects BC at F, show that
(i)ar(△BDE)=14ar(△ABC)
(ii)ar(△BDE)=12ar(△BAE)
(iii)ar(△ABC)=2ar(△BEC)
(iv)ar(△BFE)=ar(△AFD)
(v)ar(△BFE)=2ar(△FED)
(vi)ar(△FED)=18ar(△AFC).

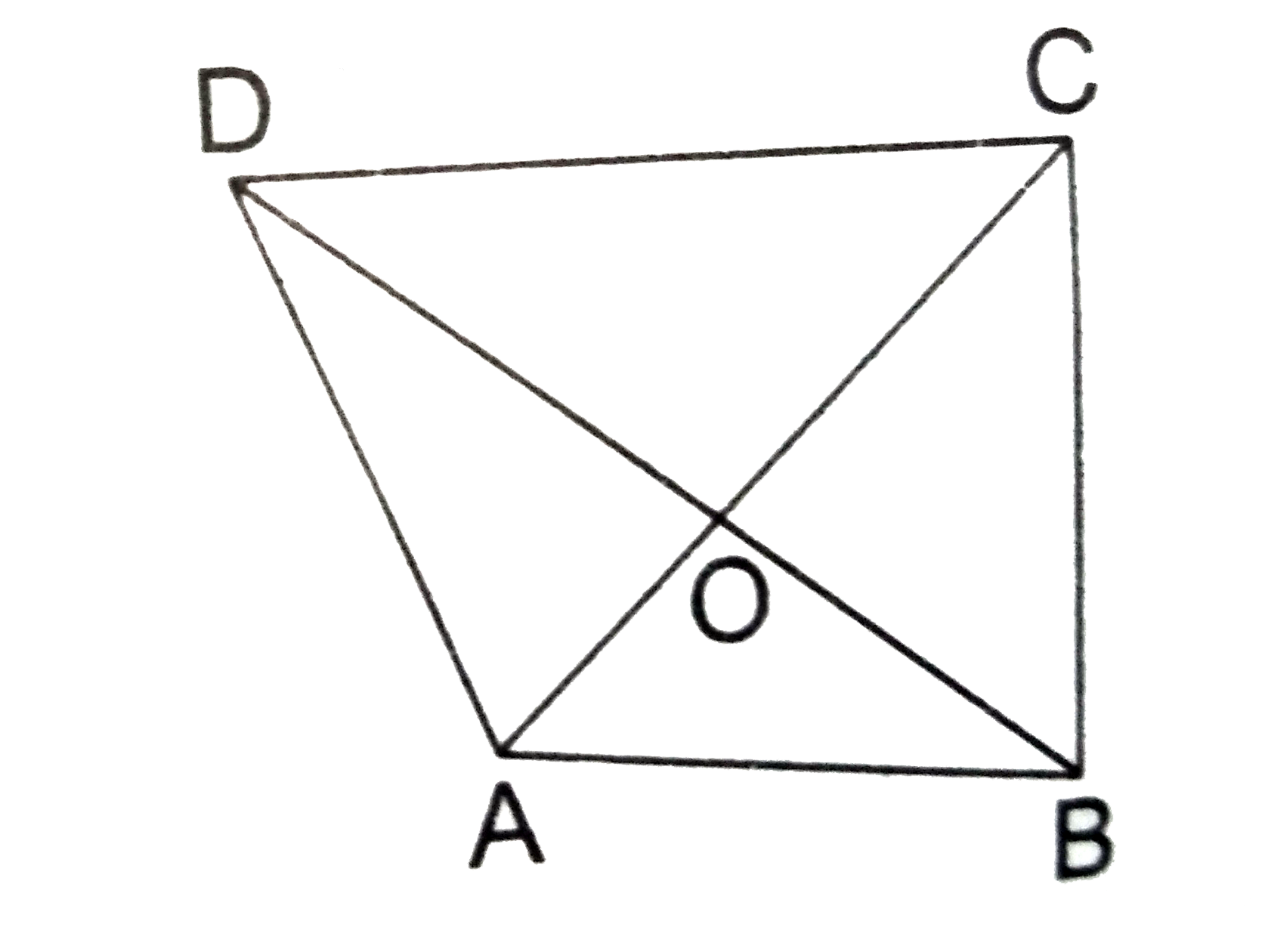
View SolutionIn the adjoining figure, the diagonals AC and BD of a quadrilateral ABCD intersect at O.
If BO=OD, prove that
ar(△ABC)=ar(△ADC).
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View SolutionLet ABCD be a tetrahedron such that the edges AB, AC and AD are mutually perpendicular. Let the area of △ABC,△ACDand△ABD be 3, 4 and5 sq. units, respectively. Then, the area of the △BCD. Is
View SolutionIf ABCD is a tetrahedron such that each △ABC,△ABDand△ACD has a right angle at A. If ar(△(ABC))=k1,ar(△ABD)=k2,ar(△BCD)=k3, then ar(triangleACD) is
View SolutionIn △ABC,∠B=60∘ and ∠C=75∘. If D is a point on side BC such that ar(△ABD)ar(△ACD)=1√3
find ∠BAD
View SolutionIf △ABC~△DEF,ar(△DEF)=100cm2andABDE=12, then ar(DABC) is
View SolutionIn △ABC, point D lies on side BC. E is the midpoint of AD. Prove that,
ar(EBC)=12ar(ABC)
View SolutionIn △ABC,∠B=60∘ and ∠C=75∘. If D is a point on side BC such that ar(△ABD)ar(△ACD)=1√3
find ∠BAD
View SolutionLet ABCD be a tetrahedron such that the edges AB, AC and AD are mutually perpendicular. Let the area of triangleABC, triangleACD and triangleABD be 3, 4 and5 sq. units, respectively. Then, the area of the triangleBCD . Is
View SolutionIf ABCD is a tetrahedron such that each △ABC,△ABDand△ACD has a right angle at A. If ar(△(ABC))=k1,ar(△ABD)=k2,ar(△BCD)=k3, then ar(△ACD) is
View SolutionIn figure, ABC and ABD are two triangles on the same base AB. If line segment CD is bisected by AB at O , show that ar (triangleABC)=ar(triangleABD) .
View SolutionD,E and F are mid-points of the sides BC, CA and AB respectively of triangleABC . Prove that ar(||gmBDEF)= 1/2 ar (triangleABC)
View SolutionABCD is trapezium in which AB||DC . DC is produced to E such that CE = AB, prove that ar(triangleABD) = ar(triangleBCE)
View Solution

