The ellipse x2+4y2=4 is inscribed in a rectangle aligned with the coordinate axes, which in turn is inscribed in another ellipse that passes through the point (4, 0). Then the equation of the ellipse is (1) x2+16y2=16 (2) x2+12y2=16 (3) 4x2+48y2=48 (4) 4x2+64y2=48Solution in Tamil
x2+16y2=16
x2+12y2=16
4x2+48y2=16
4x2+64y2=48
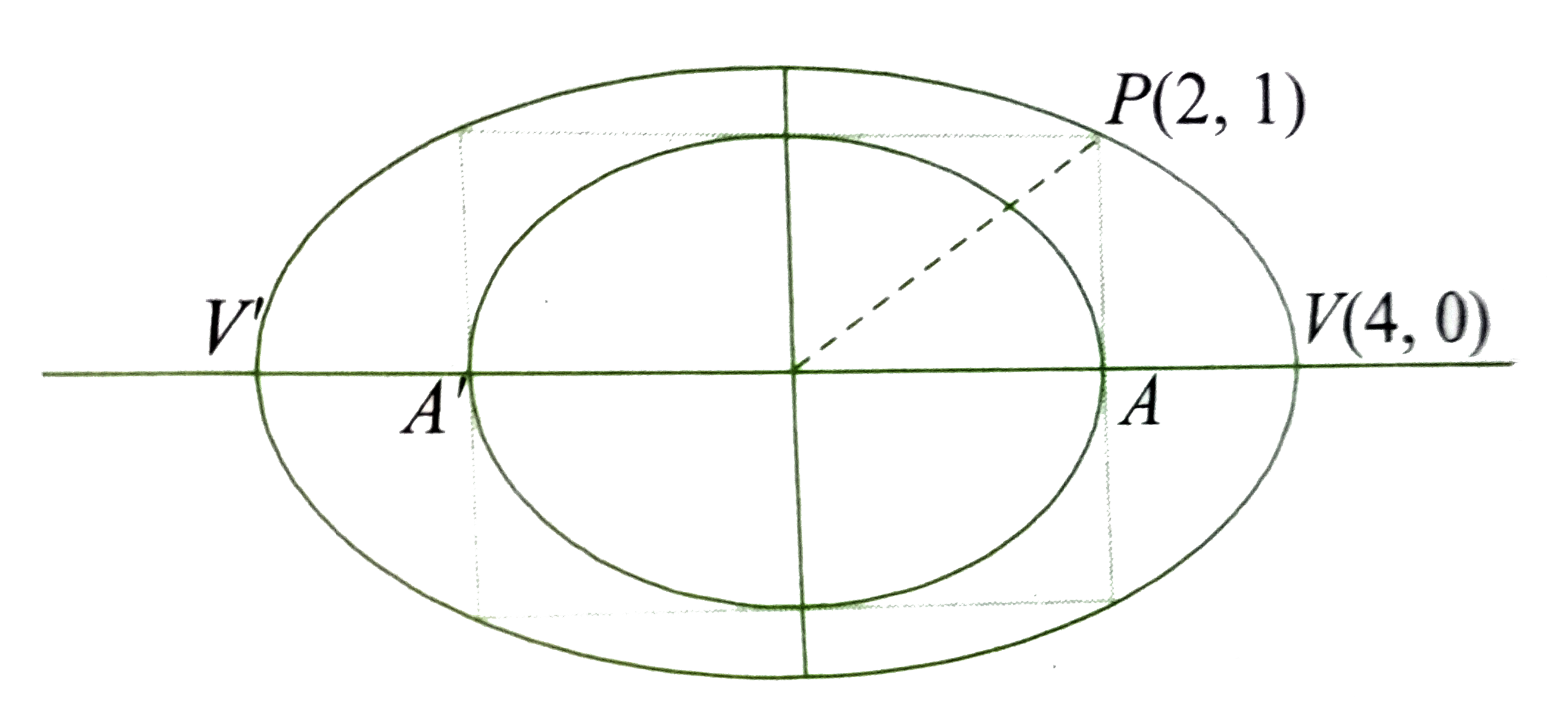
x2+4y2=4⇒x24+y21=1
So, a=2,b=1
Thus P is (2,1)
The required ellipse is x2a2+y2b2=1⇒x242+y2b2=1
The point (2,1) lis on it.So
416+1b2=1⇒1b2=1−14=34⇒b2=43
∴x216+y2(43)=1⇒x216+3y24=1⇒+12y2=16
Similar Questions
An ellipse is drawn by taking a diameter of the circle (x−1)2+y2=1 as its semi-minor axis and a diameter of the circle x2+(y−2)2=4 as its semi-major axis. If the centre of the ellipse is the origin and its axes are the coordinate axes, then the equation of the ellipse is (1) 4x2+y2=4 (2) x2+4y2=8 (3) 4x2+y2=8 (4) x2+4y2=16
View SolutionArea bounded by the ellipse x24+y216=4 is …….
View SolutionArea bounded by the ellipse x24+y216=4 is …….
View SolutionThe area of the rectangle of maximum area inscribed in the ellipse x225+y216=1 is
View SolutionThe equation of the ellipse with focii(0 , +-4) and vertices (0,+-7) isx216−y216=1 .
View SolutionThe eccentricity of te ellipse x216+y24=1 is _______
View SolutionEquation of the auxilary circle of the ellipse 3x2+4y2+6x+16y−29=0 is
View SolutionThe product of the slopes of the common tangents of the ellipse x2+4y2=16 and the parabola y2−4x−4=0 is
View Solution
