Question

Let P be a pooint on the ellipse $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b)$ in the first or second quadrants whowse foci are $S_1\text{and}{S}_2$. Then the least possible value of circumradius of $\Delta P{S}_1{S}_2$ will be

Options

A. ae
B. be
C. `(ae)/(b)`
D. `(ae^(2))/(b)`

Explanation

We known that circumradius of triangle
`R=("Product of all sides")/(4xx"Area of triangle")` ltbr Consider point `P(a cos theta, b sin thea)` on the ellipse.

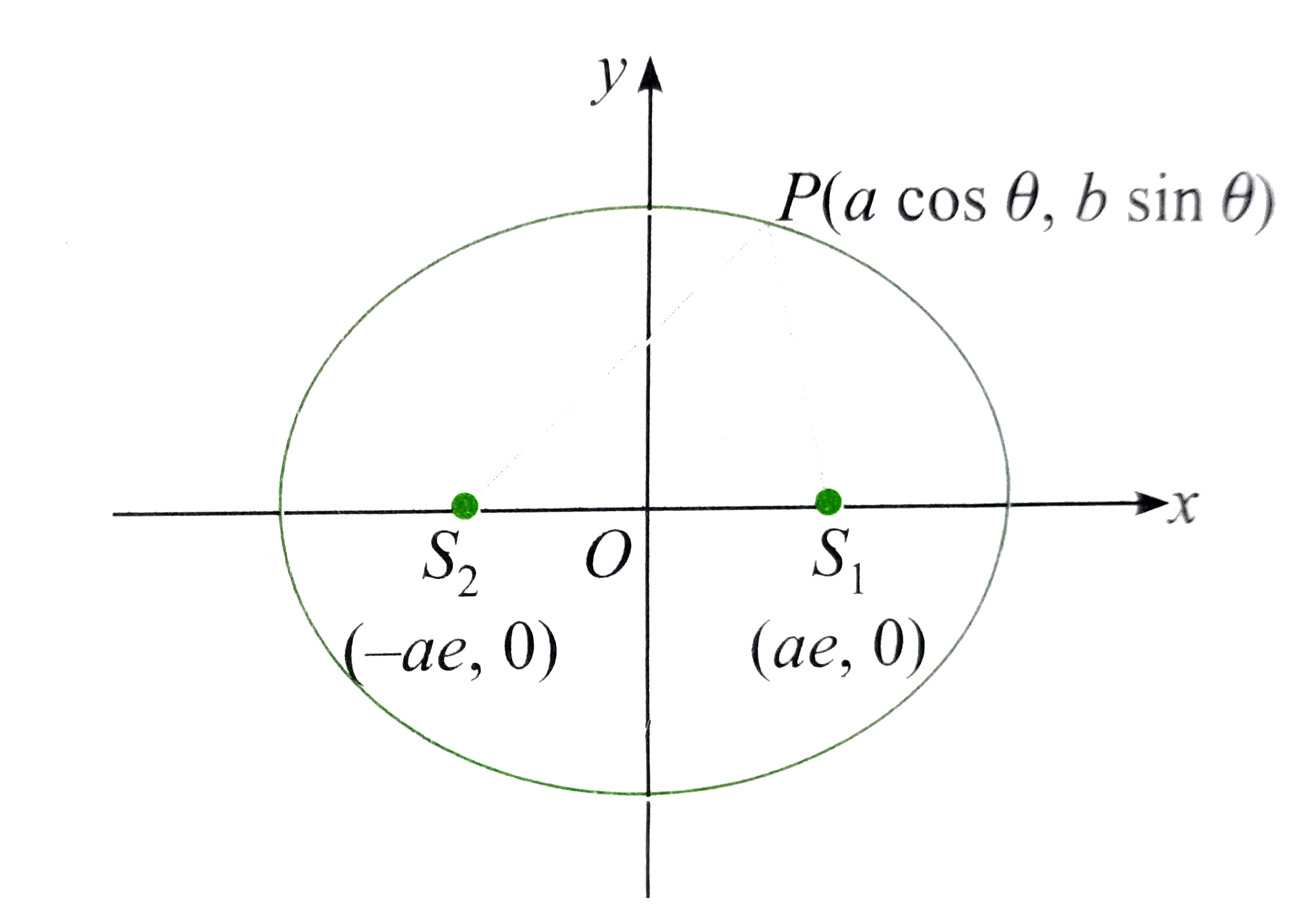
`:.` Circumrdius , `R=(a(1-ecostheta)xxa(1+ecostheta)xx2ae)/(4xx(1)/(2)b sin thetaxx2ae)`
`=(a^(2)(1-e^(2)cos^(2)theta))/(2b sin theta)`
`=(a^(2)(1-e^(2)(1-sin^(2)theta)))/(2b sin theta)`
`=(a^(2))/(2)(e^(2)sintheta+(b^(2))/(a^(2))"cosec"theta)`
`ge(a^(2))/(2b)xx(2be)/(a)ae`
`:.R_("min")=(a^(2))/(2b)xx(2be)/(a)=ae`