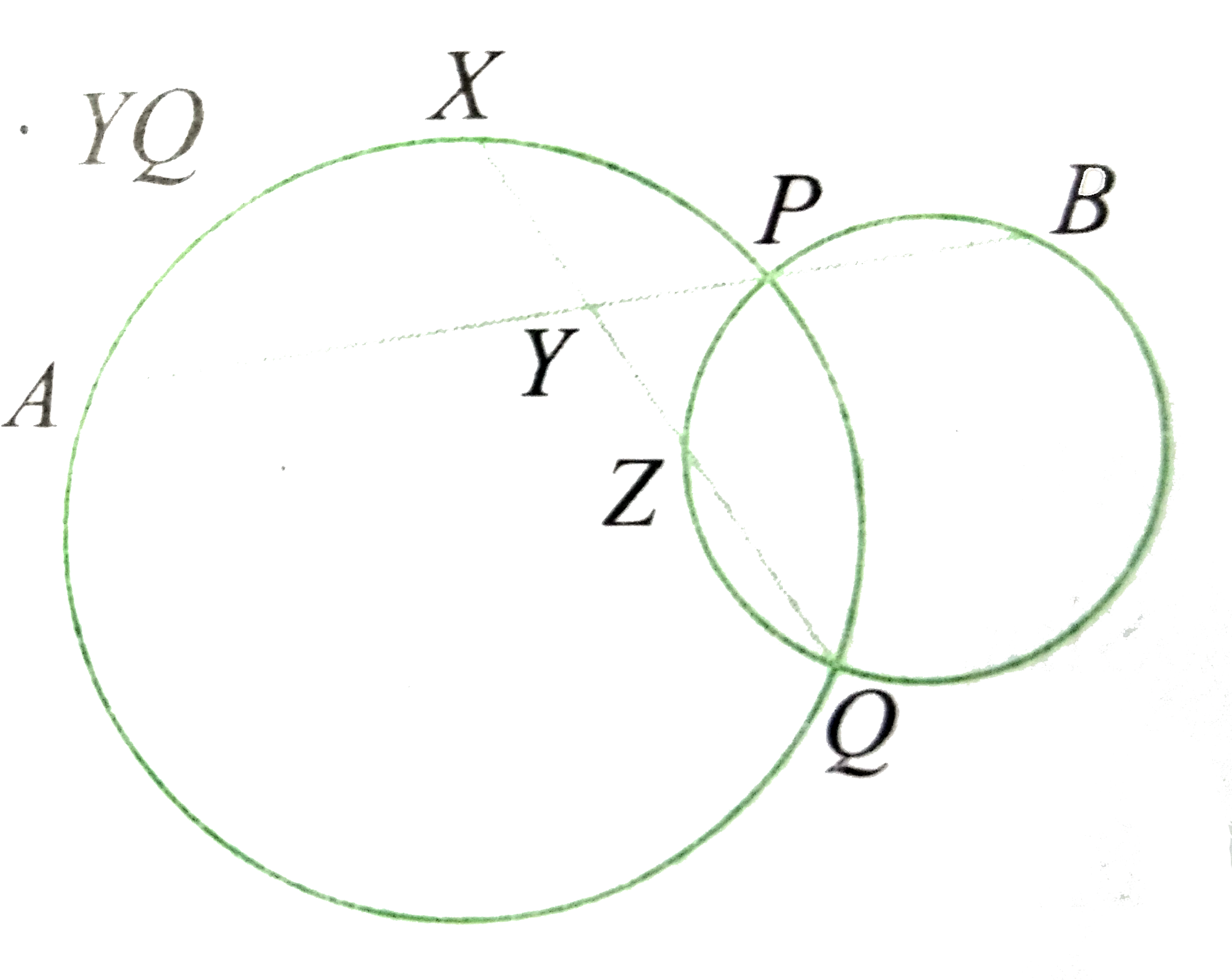
Two circles C1andC2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB,andQY meets circles C1andC2 at XandZ , respectively. Then prove that Y is the midpoint of XZ.Solution in Tamil
From the figure, YP.YB=YZ.YQ
and YA.YP=YX.YQ
But YA=YB
Hence, XY=YZ
So, Y is midpoint of XZ.
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionThe tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
View SolutionTwo circles C1andC2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB,andQY meets circles C1andC2 at XandZ , respectively. Then prove that Y is the midpoint of XZ.
View SolutionTwo circles C1 and C2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB and QY meets circles C1 andC2 at Xa n dZ respectively. Then prove that Y is the midpoint of XZ
View SolutionC1 and C2 are circle of unit radius with centers at (0, 0) and (1, 0), respectively, C3 is a circle of unit radius. It passes through the centers of the circles C1andC2 and has its center above the x-axis. Find the equation of the common tangent to C1andC3 which does not pass through C2.
View SolutionTwo circles C1andC2 both pass through the points A(1,2)andE(2,1) and touch the line 4x−2y=9 at BandD, respectively. The possible coordinates of a point C, such that the quadrilateral ABCD is a parallelogram, are (a,b). Then the value of |ab| is_________
View SolutionA tangent at a point on the circle x2+y2=a2 intersects a concentric circle C at two points PandQ . The tangents to the circle X at PandQ meet at a point on the circle x2+y2=b2. Then the equation of the circle is x2+y2=ab x2+y2=(a−b)2 x2+y2=(a+b)2 x2+y2=a2+b2
View SolutionTwo circles C1andC2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB,andQY meets circles C1andC2 at XandZ , respectively. Then prove that Y is the midpoint of XZ.
View SolutionA line passing through the origin O(0,0) intersects two concentric circles of radii aandb at PandQ, If the lines parallel to the X-and Y-axes through QandP, respectively, meet at point R, then find the locus of R.
View SolutionThe tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
View SolutionTwo circles C1andC2 intersect at two distinct points PandQ in a line passing through P meets circles C1andC2 at AandB , respectively. Let Y be the midpoint of AB,andQY meets circles C1andC2 at XandZ , respectively. Then prove that Y is the midpoint of XZ.
View SolutionC1 and C2 are circle of unit radius with centers at (0, 0) and (1, 0), respectively, C3 is a circle of unit radius. It passes through the centers of the circles C1andC2 and has its center above the x-axis. Find the equation of the common tangent to C1andC3 which does not pass through C2.
View SolutionA tangent at a point on the circle x^2+y^2=a^2 intersects a concentric circle C at two points Pa n dQ . The tangents to the circle X at Pa n dQ meet at a point on the circle x^2+y^2=b^2dot Then the equation of the circle is
View Solution
