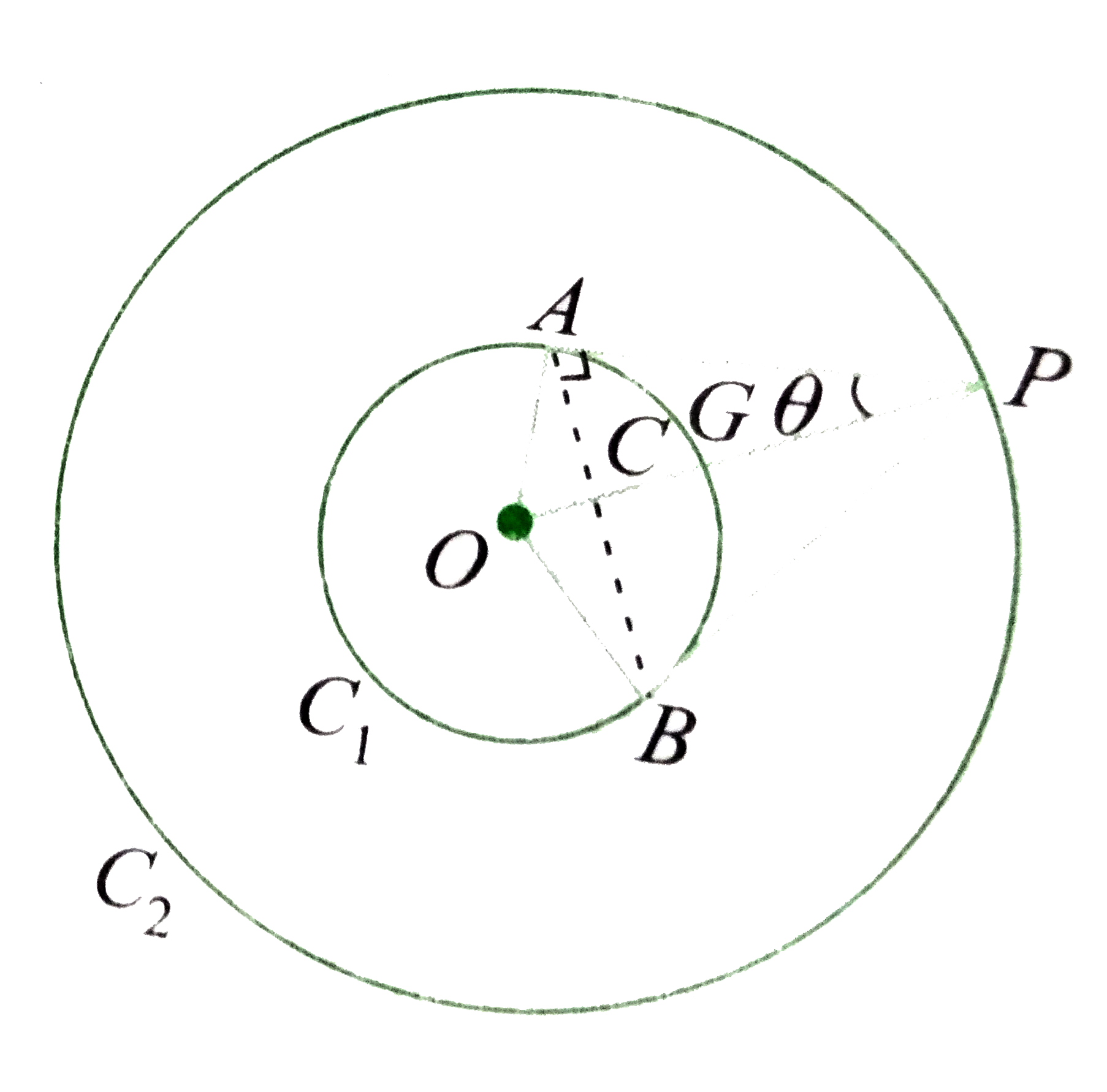
C1andC2 are two concentrate circles, the radius of C2 being twice that of C1. From a point P on C2 tangents PA and PB are drawn to C1. Prove that the centroid of the ΔPAB lies on C1Solution in Tamil
Let r be the radius of C1 and 2r be the radius of C2.Then, OA=OB=r
and OP=2r
Since PA and PB are tangents to C1,
∠OAP=∠OBP=90∘
Let OP meets C1 at G.
Let ∠OPA=θ. Then,
sinθ=OAOP=r2r=12
or θ=30∘
or ∠AOP=60∘
In ΔOAC,
cos60∘=OCOA
or 12=OCror OC=r2
∴PC=2r−r2−3r2
Also, CG=r−OC=r−r2=r2
Clearly, CG=13PC
Therefore, G is the centroid of ΔABP.
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionTransverse common tangents are drawn from O to the two circles C_(1),C_(2) with 4,2 respectively.Then the ratio of the areas of triangles formed by the tangents drawn from O to the circles C_(1) and C_(2) and chord of contacts of O w.r.t the circles C_(1) and C_(2) respectively is
View SolutionProve that (C_(0)+C_(1))(C_(1)+C_(2))(C_(2)+C_(3))(C_(n-1)+C_(n))=((n+1)^(n))/(n!)*c_(0)*C_(1)*C_(2).........
View SolutionIf C1:x2+y2=(3+2√2)2 be a circle. PA and PB are pair of tangents on C1 where P is any point on the director circle of C1, then the radius of the smallest circle which touches C1 externally and also the two tangents PA and PB is
View SolutionEvaluate ∣∣ ∣∣mC1mC2mC3nC1nC2nC3pC1pC2pC3∣∣ ∣∣
View SolutionC1andC2 are two concentrate circles, the radius of C2 being twice that of C1. From a point P on C2 tangents PA and PB are drawn to C1. Prove that the centroid of the ΔPAB lies on C1
View SolutionIf C1,C2,C3,... is a sequence of circles such that Cn+1 is the director circle of Cn. If the radius of C1 is 'a', then the area bounded by the circles Cn and Cn+1, is
View SolutionProve that : Prove that
C1C0+2.C2C1+3.C3C2+….+n.CnCn−1=n(n+1)2
View SolutionIf C0,C1,C2,…,Cn are the binomial coefficients in the expansion of (1+x)n⋅n being even, then C0+(C0+C1)+(C0+C1+C2)+….+(C0+C1+C2+…+Cn−1) is equal to :
View SolutionC_(1) And C_(2) There are two concentric circles C_(2) Radius of C_(1) Is twice the radius. C_(2) From a point P C_(1) PA and two tangents on PB Prove that the triangle is drawn PAB Center of C_(1) Is located at.
View SolutionProve that :
2C1+3C1+4C1=3C2+4C2.
View SolutionIf C1:x2+y2=(3+2√2)2 be a circle. PA and PB are pair of tangents on C1 where P is any point on the director circle of C1, then the radius of the smallest circle which touches C1 externally and also the two tangents PA and PB is
View SolutionC1andC2 are two concentrate circles, the radius of C2 being twice that of C1. From a point P on C2 tangents PA and PB are drawn to C1. Prove that the centroid of the ΔPAB lies on C1
View Solution
