Question

Find the maximum value of $f\left(x\right)={\left(\frac{1}{x}\right)}^x$

Explanation

We have `f(x) = (1/x)^(x)`
Clearly, domain of the function is `x gt 0`
Differentiating we get, `f^(')(x)=(1/x)^(x)(log1/x-1)`
`f^(')(x) =0 rArr log1/x=1 = log_(e)e rArr 1/x=e rArr x=1/e`
Also for `x lt 1//e, f^(')(x)` is positive and for `x gt 1//e, f^(')(x)` is negative.
Therefore, the maximum value of the function is `e^(1//e)`.
Also, `underset(x to 0)"lim"(1/x)^(x) = e^(underset(xto0)"lim"xlog(1/x))=e^(underset(xto0)"-lim"xlogx)=e^(underset(xto0)-"lim"(logx)/(1/x))=e^(underset(xto0)-"lim"(1/x)/(-1/x^(2)))=e^(0)=1`
`underset(xto infty)"lim"(1/x)^(x)=0`
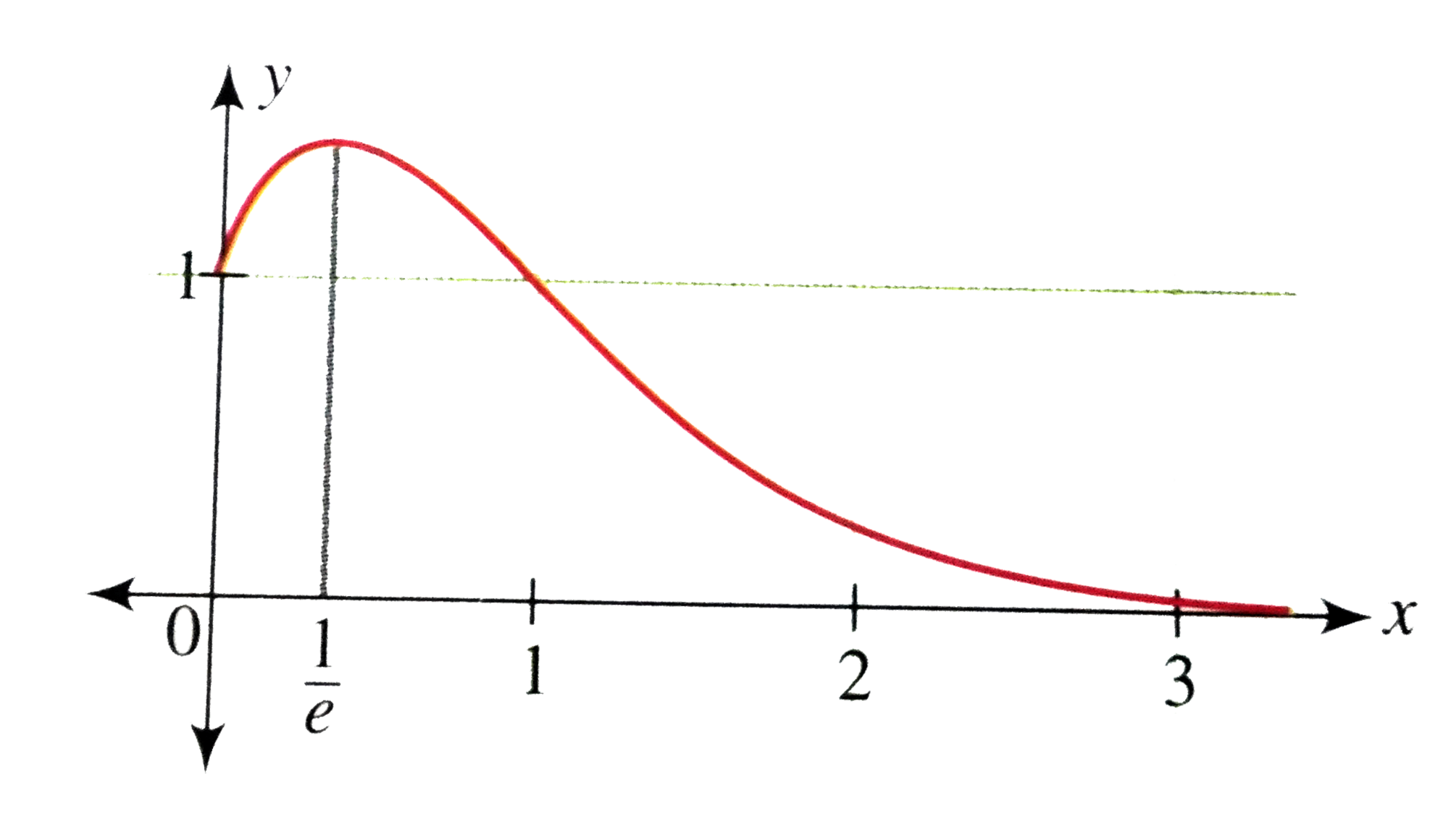
From the above discussion, the graph of the function is as shown in the following figure.