Question

Compute the area of the region bounded by the curves $y=ex\left({\log }_{e}x\right)\text{and}y=\frac{{\log }_{e}x}{ex}$

Answer

`((4-sqrt(2))/log 2-(5)/(2) log 2+(3)/(2))`sq. units

Explanation

The given curves are
`x=(1)/(2)`
`x=2`
`y=log_(e)x`
`y=2^(x)`

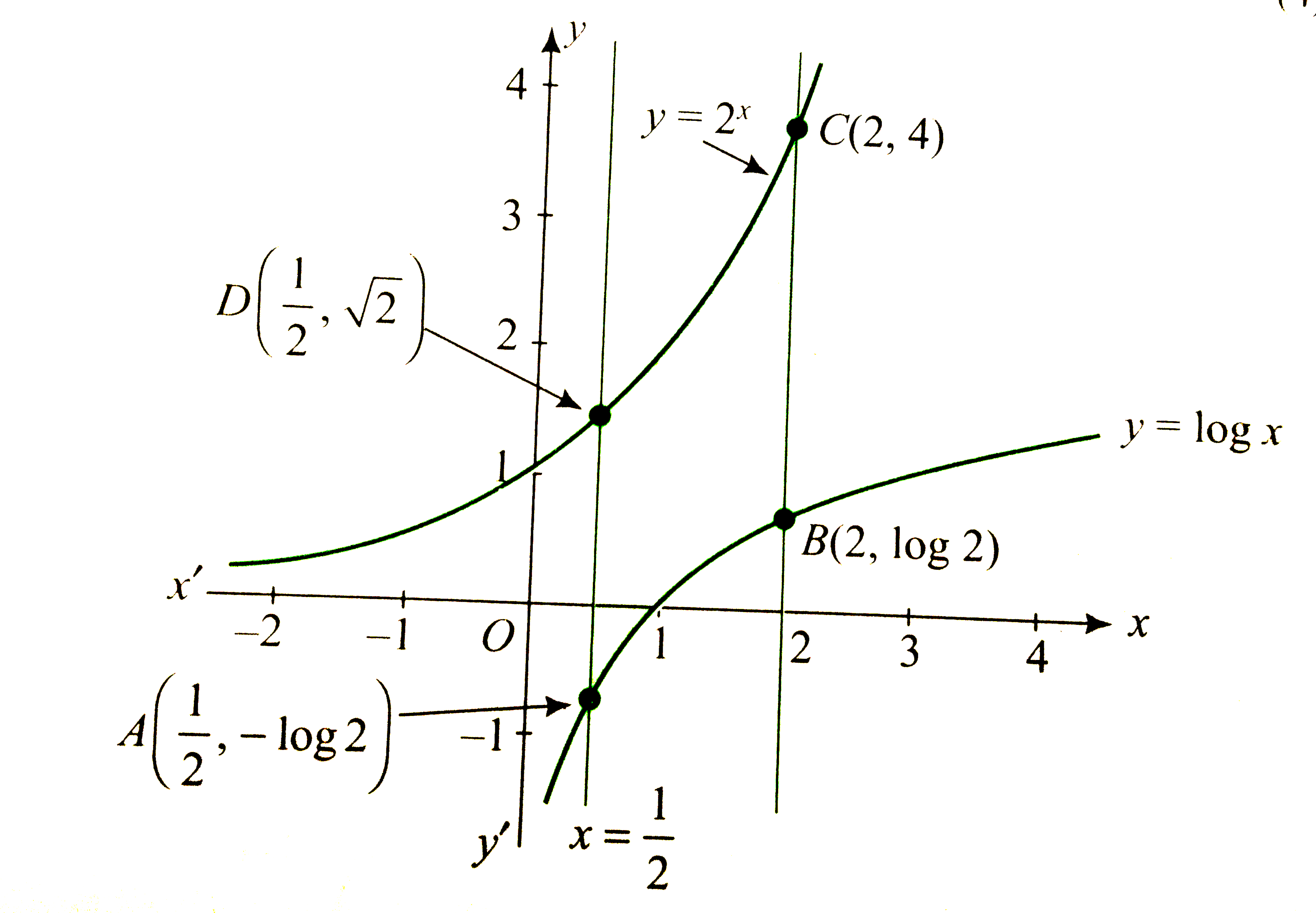
Required area = Area of ABCDA
`=int_(1//2)^(2)(2^(x)-log x)dx`
`[(2^(x))/(log 2)-(x log x -x)]_(1//2)^(2)`
`=((4)/(log 2)-2 log 2+2)-(-(sqrt(2))/(log 2)-(1)/(2)log""(1)/(2)+(1)/(2))`
`=((4-sqrt(2))/(log 2)-(5)/(2)log 2 +(3)/(5))` sq. units.