Let f(x)+f(y)=f(x√1−y2+y√1−x2)[f(x) is not identically zero]. Then f(4x3−3x)+3f(x)=0 f(4x3−3x)=3f(x) f(2x√1−x2+2f(x)=0 f(2x√1−x2=2f(x)Solution in Tamil
f(4x3−3x)+3f(x)=0
f(4x3−3x)=3f(x)
f(2x√1−x2)+2f(x)=0
f(2x√1−x2)=2f(x)
The correct Answer is:A, D
Given f(x)+f(y)=(x√1−y2+y√1−x2) (1)
Replace y by x. Then 2f(x)=f(2x√1−x2)
3f(x)=f(x)+2f(x)
=f(x)+f(2x√1−x2)
=f(x√1−4x2(1−x2)+2x√1−x2√1−x2)
=f(x√(2x2−1)2+2x(1−x2))
=f(x∣∣2x2−1∣∣+2x−2x3)
=f(2x3−x+2x−2x3)orf(x−2x3+2x−2x3)
=f(x)orf(3−4x3)
∴f(x)=0or3f(x)=f(3x−4x3)
Consider 3f(x)=f(3x−4x3)
Replacing x by -x, we get
3f(−x)=f(4x3−3x) (2)
Also, from (1),f(x)+f(−x)=f(0).
Putting x=y−0 in (1), we have f(0)=0 or f(x)+f(−x)=0.
Thus, f(x) is an odd function.
Now, from (2), −3f(x)=f(4x3−3x)
or f(4x3−3x)=3f(x)=0
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Comprehension)
32 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Matrix)
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise (Single)
125 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Consider the functions
f(x)={x+1,x≤12x+1,1<x≤2andg(x)={x2,−1≤x<2x+2,2≤x≤3
The domain of the function f(g(x)) is
View SolutionThe function f(x) is defined on the interval [0, 1]. Now, match the following lists:
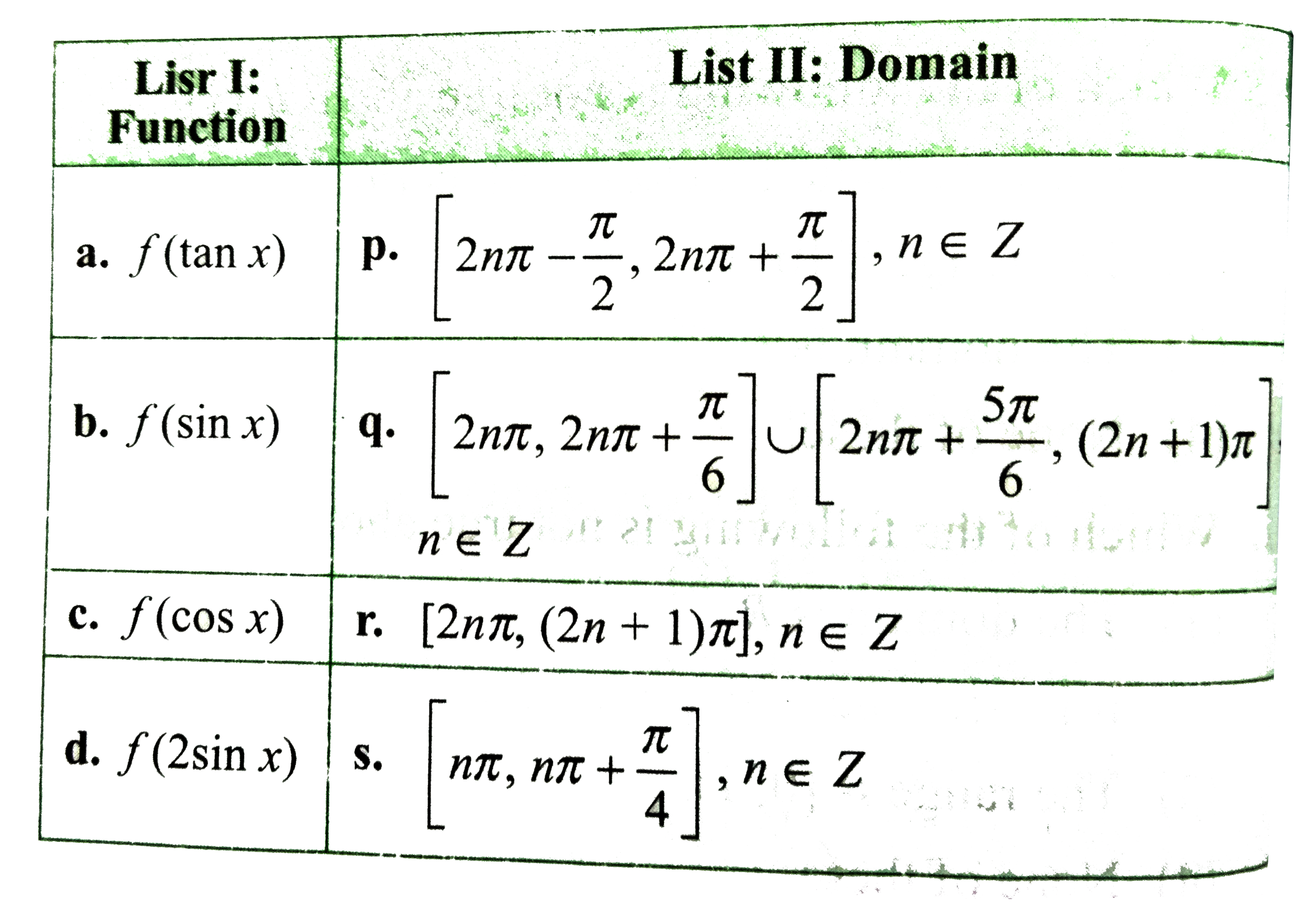
View SolutionThe relation R={(1,1),(2,2),(3,3),(1,2),(2,3),(1,3)} on a set A={1, 2, 3} is
View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
View SolutionLet f(x)+f(y)=f(x√1−y2+y√1−x2)[f(x) is not identically zero]. Then f(4x3−3x)+3f(x)=0 f(4x3−3x)=3f(x) f(2x√1−x2+2f(x)=0 f(2x√1−x2=2f(x)
View SolutionLet f(x+(1)/(y))+f(x-(1)/(y))=2f(x)f((1)/(y))AA x,y in R,y!=0 and f(0)=0 then the value of f(1)+f(2)=
View SolutionLet f(x) be twice differentiable function such that f'(0)=2, then, limx→02f(x)−3f(2x)+f(4x)x2, is
View Solutionयदि 2f(x)−3f(1x)=x2(x≠0), तब f(2)=
View SolutionLet f(x) be a twice differentiable function and f11(0)=2, then Limx→02f(x)−3f(2x)+f(4x)x2 is
View SolutionIf 2f(x)=f(2x),3f(x)=f(3x),4f(x)=f(4x)……. etc. then f(1)+f(2)+f(3)+……..+f(n) equals to where f(1)=1 :
View SolutionLet 3f(x)−2f(1x)=x the f'(2) is equal to
View SolutionLet f(x)+f(y)=f(x√1−y2+y√1−x2)[f(x) is not identically zero]. Then f(4x3−3x)+3f(x)=0 f(4x3−3x)=3f(x) f(2x√1−x2+2f(x)=0 f(2x√1−x2=2f(x)
View SolutionLet f(x) be a twice-differentiable function and f(0)=2. The evaluate: (lim)x→02f(x)−3f(2x)+f(4x)x2
View SolutionLet f(x+1y)+f(x−1y)=2f(x)f(1y)∀x,y∈R,y≠0 and f(0)=0 then the value of f(1)+f(2)=
View SolutionLet f(x) be a twice-differentiable function and f''(0)=2. Then evaluate limx→02f(x)−3f(2x)+f(4x)x2.
View Solution
