Question

Solve $\sin x\succ \frac{1}{2}\text{or}$
find the domain of $f\left(x\right)=\frac{1}{\sqrt{1+2\sin x}}$

Explanation

To define `f(x)`, we must have `1+2sin x gt 0 or sinx gt -(1)/(2).`
The function `sin x` has the least positive period `2 pi`. That is why it is sufficient to solve the inequalities of the form ` sinx gt a,sinx ge a, sinx lt a, and x le a ` first on the interval of length `2 pi`, and then get the solution set by adding numbers of the form ` 2pi n, n in Z, ` to each of the solutions obtained on that interval.
Thus, let us solve this inequality on the interval `[-(pi)/(2),(3pi)/(2)]`.

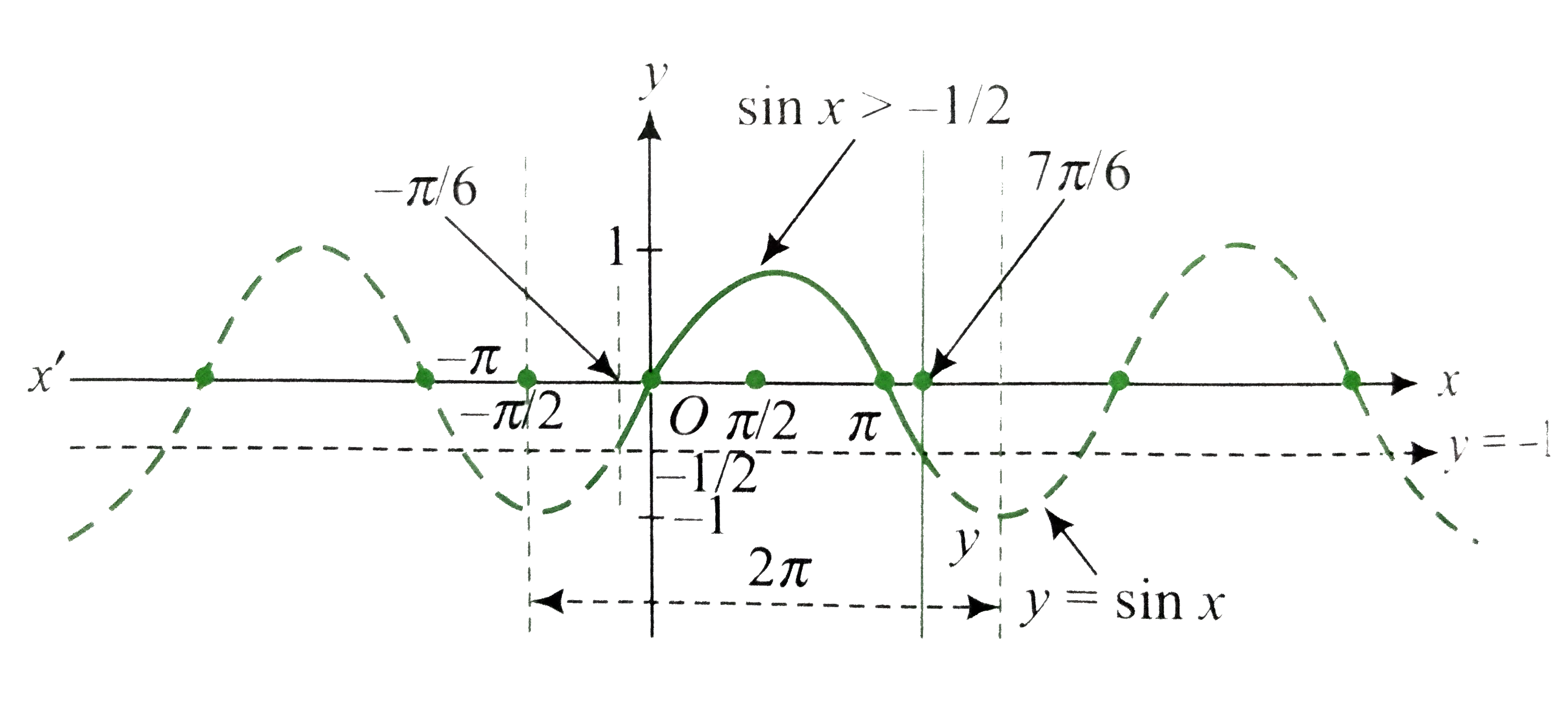
From the figure,
`sinx gt -(1)/(2) " when " -(pi)/(6) ltx lt(7pi)/(6)`
Thus, on generalizing the above solution, we get
` x in underset(n inz)(cup)((-pi)/(6)+2n pi,(7pi)/(6)+2n pi)`