If z=(3+7i)(a+ib), where a, b∈Z−{0}, is purely imaginery, then minimum value of |z|2 isSolution in Tamil
74
45
65
58
The correct Answer is:D
(d) z=(3a−7b)+i(3b+7a)
For purely imaginary, 3a=7b
⇒a=7 or b=3 (for least value of |z|)
⇒|z|=|3+7i|=√58
Topper's Solved these Questions
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Multiple Correct Answer
11 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Matching Column
1 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
- CONIC SECTIONSBOOK - CENGAGECHAPTER - CONIC SECTIONSEXERCISE - Solved Examples And Exercises
87 Videos
Similar Questions
Complex numbers whose real and imaginary parts x and y are integers and satisfy the equation 3x2−|xy|−2y2+7=0
View Solutionz1, z2, z3 are vertices of a triangle. Match the condition in List I with type of triangle in List II.
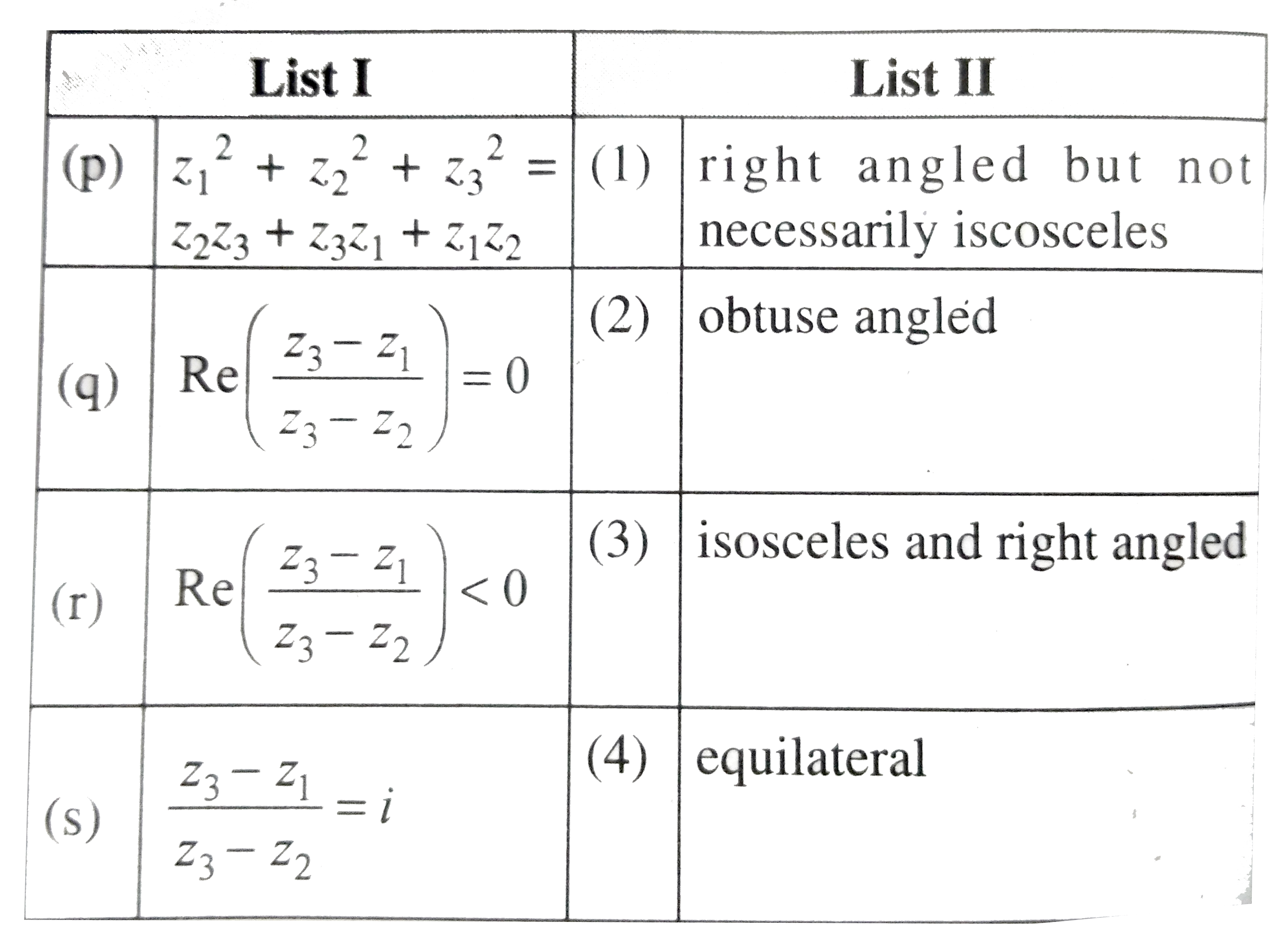
Codes
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionGiven that A(1,1) and B(2,−3) are two points and D is a point on AB produced such that AD=3AB. Find the coordinates of D.
View SolutionIf z=(3+7i)(a+ib), where a, b∈Z−{0}, is purely imaginery, then minimum value of |z|2 is
View SolutionIf z=(3+7i)(a+ib) where a,b∈∈Z−{0}, is purely imaginary , then the minimum value of |z| is
View SolutionIf z=(3+7i)(λ+iμ), when λ,μ∈I−{0} and i=√−1, is purely imaginary then minimum value of |z|2 is
View SolutionFor a complex number z
A) Minimum value of |z|+|z-2| B) Minimum value of |z-1|+|z-2|
C) Minimum value of |z-2|+|z-6| D) Minimum value of |z-1|+|z-4|
Arrange the above values in ascending order
View Solutionयदि z=x+iy,z13=a−ib तथा xa−yb=k(a2−b2) जहाँ k =
View SolutionLet O=(0,0),A=(3,0),B=(0,−1) and C=(3,2), then the minimum value of |z|=|z−3|+|z+i|+|z−3−2i| occurs at the (where, z is complex number)
View SolutionThe minimum value of |z−2|+|z−3| is
View SolutionIf z=(3+7i)(a+ib), where a, b∈Z−{0}, is purely imaginery, then minimum value of |z|2 is
View SolutionIf z=(3+7i)(λ+iμ), when λ,μ∈I−{0} and i=√−1, is purely imaginary then minimum value of |z|2 is
View Solutionमाना कि O = (0, 0), A = (3, 0), B = (0, – 1) और C = (3, 2) है, तब |z|+|z−3|+|z+i|+|z−3−2i| का न्यूनतम मान निम्न पर प्राप्त होता है (जहाँ z एक सम्मिश्र संख्या है) -
View SolutionIf z=(3+7i)(λ+iμ), when λ,μ∈I−{0} and i=√−1, is purely imaginary then minimum value of |z|2 is
View Solution
