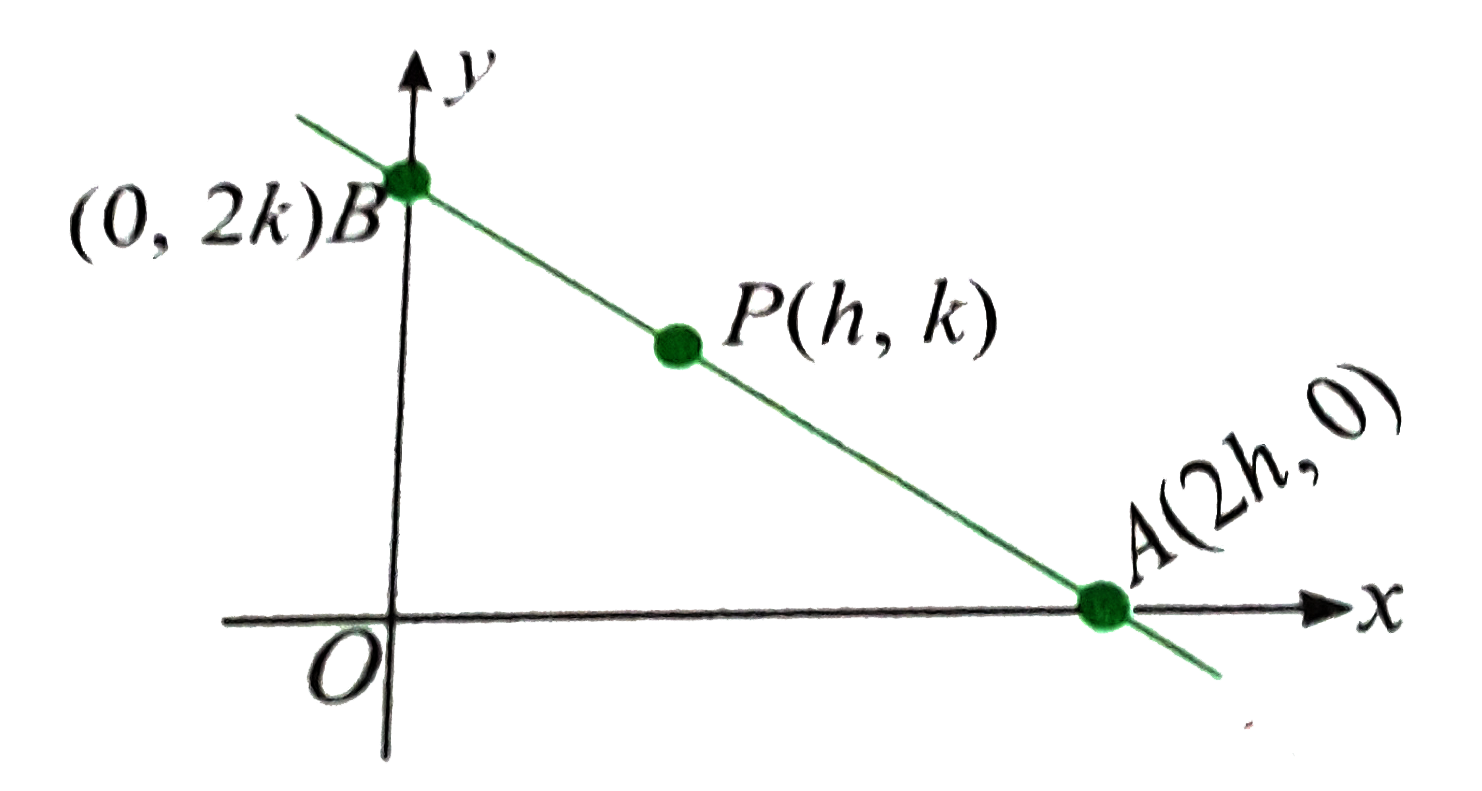
A variable line through point meets the axes at . Find the locus of the circumcenter of triangle (where is the origin).Solution in Tamil
The correct Answer is:
Since triangle OAB is right-angled, its circumcenter is the midpoint of hypotenuse AB.
So, let the midpoint of AB be .
Then the coordinates of A and B are and respectively. Now, points A,B and P are collinear. Therefore,
or
or
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Single)
59 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise (Multiple)
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.5
5 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
ABC is an isosceles triangle. If the coordinates of the base are B(1,3) and C(−2,7) , the coordinates of vertex A can be (a)(1,6) (b) (−12,5) (c)(56,6) (d) none of these
View SolutionIf (−6,−4),(3,5),(−2,1) are the vertices of a parallelogram, then the remaining vertex can be (0,−1) (b) 7,9) (−1,0) (d) (−11,−8)
View SolutionConvert the following polar coordinates to its equivalent Cartesian coordinates.
(i) (2,π)
(ii) (√3,π/6)
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionA variable line through the point P(2,1) meets the axes at AandB . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionA variable line through point P(2,1) meets the axes at AandB . Find the locus of the circumcenter of triangle OAB (where O is the origin).
View SolutionA variable line intersects the co-ordinate axes at A and B and passes through a fixed point (a,b). then the locus of the vertex C of the rectangle OACB where O is the origin is
View SolutionA line passing through P(4,2) meet the X and Y -axes at A and B, respectively.If O is the origin,then locus of the centre of the circumference of triangle OAB is
View SolutionThe variable line drawn through the point (1,3) meets the x -axis at A and y -axis at B .If the rectangle OAPB is completed.Where O isthe origin,then locus of ^(-)P' is
View SolutionA variable circle having fixed radius 'a' passes through origin and meets the co-ordinate axes in point A and B. Locus of centroid of triangle OAB where 'O' being the origin, is -
View SolutionA variable line passing through a fixed point (α,β) intersects the coordinate axes at A and B. If O is the origin, then the locus of the centroid of the ΔOAB is
View SolutionA variable line intersects the co-ordinate axes at A and B and passes through a fixed point (a, b), then the locus of the vertex C of the rectangle OACB where O is the origin is :
View SolutionA line is at a distance c from origin and meets axes in A an dB. The locus of the centre of the circle passing through O,A,B ais
View SolutionA variable line through the point P(2,1) meets the axes at A an d B . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionA variable line passing through point P(2,1) meets the axes at A and B . Find the locus of the circumcenter of triangle OAB (where O is the origin).
View Solution
