Two points $P a n d Q$ are given. $R$ is a variable point on one side of the line $P Q$ such that $∠ R P Q - ∠ R Q P$ is a positive constant $2 α .$ Find the locus of the point $R .$ Solution in Tamil

Video Solution

Text Solution

Verified by Experts

Let $R \equiv (x_{1}, y_{1})$ .
Also , let, $∠ R P M = t h e t and ∠ R Q M = ϕ$ .

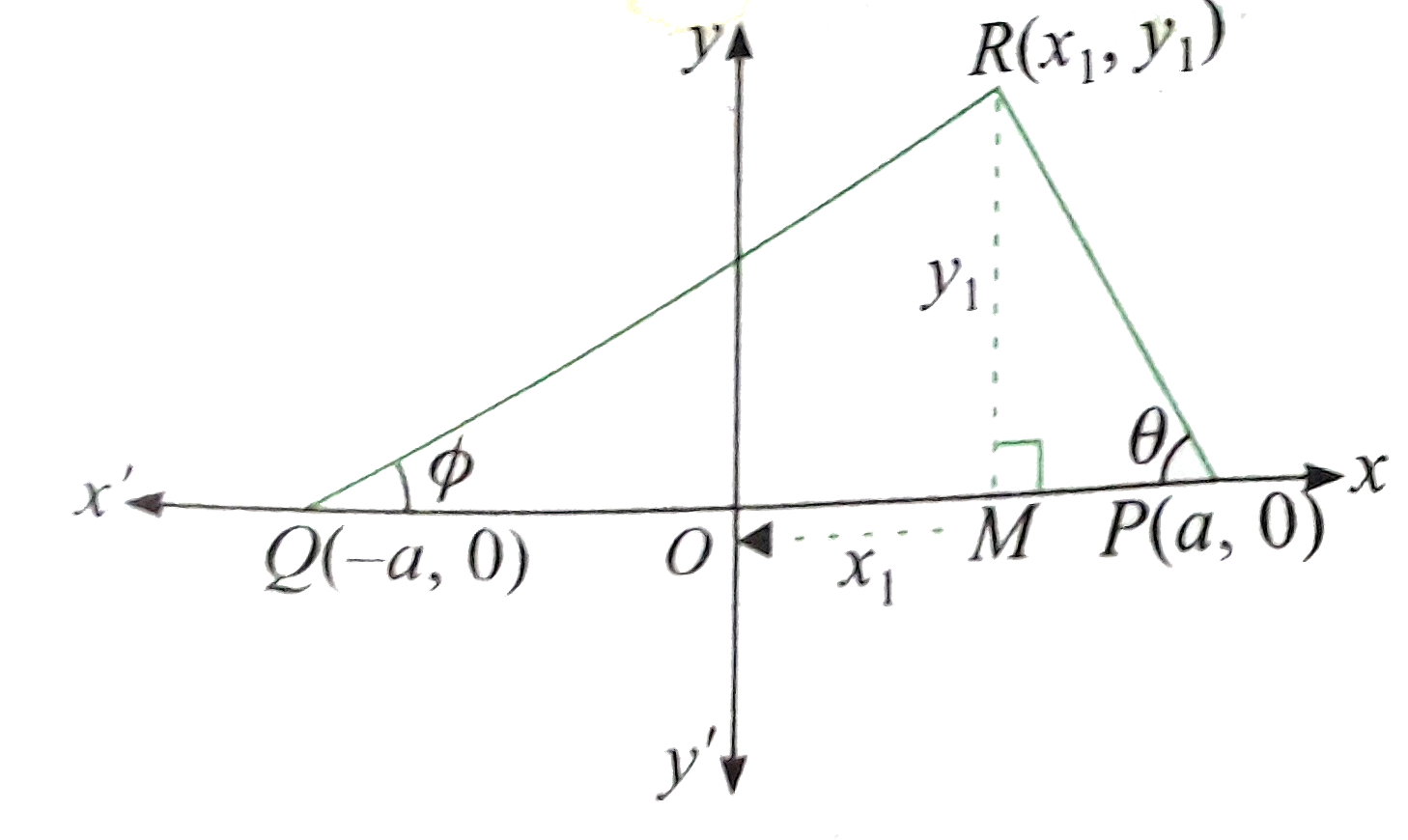
In $Δ R M P, tan θ = \frac{R M}{M P} = \frac{y_{1}}{a - x_{1}}$
In $Δ R Q M, tan θ ϕ = \frac{R M}{Q M} = \frac{y_{1}}{a + x_{1}}$
But given $∠ R P Q - a n l \geq R Q P = 2 α$ (constant).Therefore, $θ - ϕ = 2 α$
or $tan (θ - ϕ) = tan 2 α$
or $\frac{tan θ - tan θ}{1 + tan θ tan θ} = tan 2 α$
or $\frac{\frac{y_{1}}{a - x_{1}} - \frac{y_{1}}{a + x_{1}}}{1 + \frac{y_{1}}{a - x_{1}} \frac{y_{1}}{a + x_{1}}} = tan 2 α$
or $\frac{2 x_{1} y_{1}}{a^{2} = x_{1}^{2} + y_{1}^{2}} = tan α$
or $a^{2} - x_{1}^{2} + y_{1}^{2} = 2 x_{1} y_{1} cot 2 α$
or $x_{1}^{2} - y_{1}^{2} + 2 x_{1} y_{1} cot 2 α = a^{2}$
Hence, the locus of the point $R (x_{1}, y_{1})$ is $x^{2} - y^{2} + 2 x y cot 2 α = a^{2}$

Updated on:21/07/2023

|

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

CENGAGE-COORDINATE SYSYEM -JEE Main Previous Year

Home
Ask Doubt
Profile