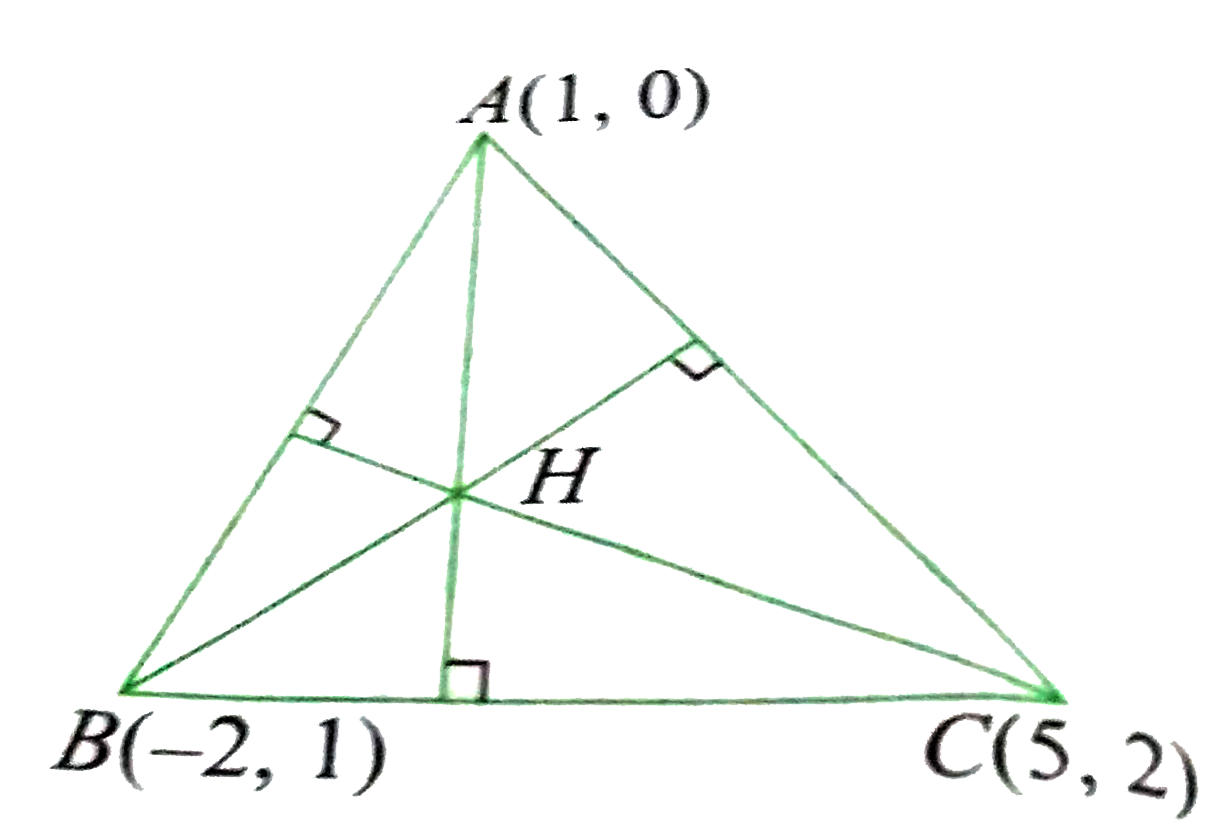
Find the orthocentre of ABC with vertices A(1,0),B(−2,1), and C(5,2)Solution in Tamil
Let the orthocenter be H(h,k).
Slope of BC=2−15−(−2)=17
Slope of AC=2−05−1=12
AH⊥BC
∴ Slope of AH=−7
or =k−0h−1=−7
∴−7h+7=k or 7h+k=7
Also, BH⊥AC
∴ Slope of BH=−2
or =k−0h+2=−2
∴k−1=−2h−4 or 2h+k=−3
Solving (1) and (2), we get h=2 and k=−7. Hence, the orthocenter is (2,−7)
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.1
6 Videos
- COORDINATE SYSYEM BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.2
8 Videos
- COORDINATE SYSTEMBOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
What is the minimum area of a triangle with integral vertices ?
View SolutionThe distance between the points (acosα,asinα) and (acosβ,asinβ) is
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionFind the orthocentre of ΔABC with vertices A(1,0),B(−2,1), and C(5,2)
View SolutionIf A(1,-1,3), B(2,1,-2), C(-5,2-6) are the vertices of a △ABC, then the lengh of internal bisector of angle A is
View SolutionIf A=[12−21],B=[233−4] and C=[10−10], verfity (i) A(B+C)=AB+AC.
View SolutionIf A=⎡⎢⎣ 1 0−2 3−1 0−2 1 1⎤⎥⎦,B=⎡⎢⎣ 05−4−21 3−10 2⎤⎥⎦ and C=⎡⎢⎣ 1 52−1 10 0−11⎤⎥⎦,
verify that A(B−C)=(AB−AC).
View Solutionयदि A=⎡⎢⎣13213−1⎤⎥⎦,B=⎡⎢⎣2112−10⎤⎥⎦ हो, तो आव्यूह C ज्ञात कीजिये, यदि A+B+C=0
View Solutionयदि A=[1221],B=[2334] और C=[1010], हों तो सत्यापित कीजिए :
A(B+C)=AB+AC
View SolutionIf A=(1021) and A10=(abcd)then a+b+c+d
View SolutionIf A=[1021] and A2012=[abcd] then find the values of a,b,c and d.
View SolutionIf A=[12−21],B=[233−4] and C=[10−10], verfity (i) A(B+C)=AB+AC.
View SolutionFind the orthocentre of ΔABC with vertices A(1,0),B(−2,1), and C(5,2)
View SolutionFind the orthocentre of ΔABC with vertices A(1,0),B(−2,1), and C(5,2)
View SolutionIf A=[543−1],B=[2104]andC=[−3210], find :
(i) A+C (ii) B-A (iii) A+B-C
View Solution
