Consider function f(x)=sin−1(sinx)+cos−1(cosx),x∈[0,2π]
(a) Draw the graph of y=f(x)
(b) Find the range of f(x)
(c) Find the area bounded by y=f(x) and x-axisSolution in Tamil
The correct Answer is:Range is [0,π], Area =π2 sq. units
f(x)=sin−1(sinx)+cos−1(cosx)
=x+x=2xx∈[0,π/2]=π−x+x=πx∈[π/2,π]=π−x+2π−x=3π−2xx∈[π,3π/2]=x−2π+2π−x=0x∈[3π/2,2π]
Graph of the function is as shown in the following figure
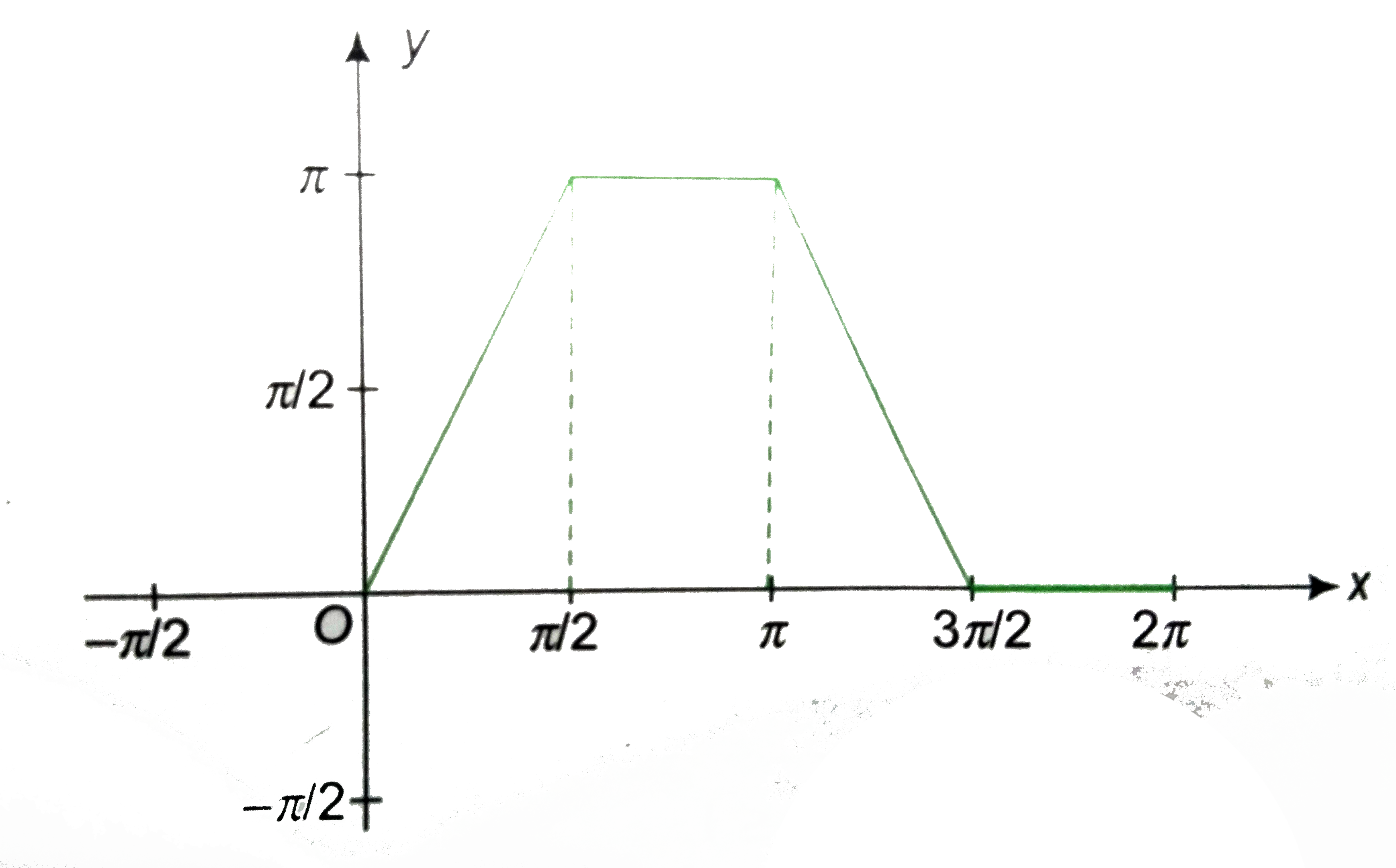
From the graph, rangle is [0,π]
Also, area bounded by y=f(x) and x -axis is,
A=12(3π2+π2)(π)
π2 sq. units
Topper's Solved these Questions
Similar Questions
Find the values of λ such that x,y,z≠(0,0,0)and(ˆi+ˆj+3ˆk)x+(3ˆi−3ˆj+ˆk)y+(−4ˆi+5ˆj)z=λ(xˆi+yˆj+zˆk),whereˆi,ˆjandˆk are unit vector along coordinate axes.
View SolutionIf y = y(x) is the solution of the differential equation, xdydx+2y=x2 satisfying y(1) = 1, then y(12) is equal to
View SolutionThe area bounded by the curve y=f(x), the x -axis and x=1 and x=c is (c-1)sin(3c+4) Then f(x) is
View Solutionf(x)=(1)/(sin x cos x) find ,f'(x)=?
View SolutionConsider function f(x)=sin−1(sinx)+cos−1(cosx),x∈[0,2π]
(a) Draw the graph of y=f(x)
(b) Find the range of f(x)
(c) Find the area bounded by y=f(x) and x-axis
View SolutionThe area bounded by the graph of y=f(x),f(x)>0 on [0,a] and x-axis is a22+a2sina+π2cosa then find the value of f(π2).
View Solutionयदि F(x)=⎡⎢⎣cosx−sinx0sinxcosx0001⎤⎥⎦ है तो सिद्ध कीजिए कि F(x)F(y)=F(x+y)
View SolutionLet f(x)=max{sinx,cosx,12}, then determine the area of region bounded by the curves y=f(x), X-axis, Y-axis and x=2π.
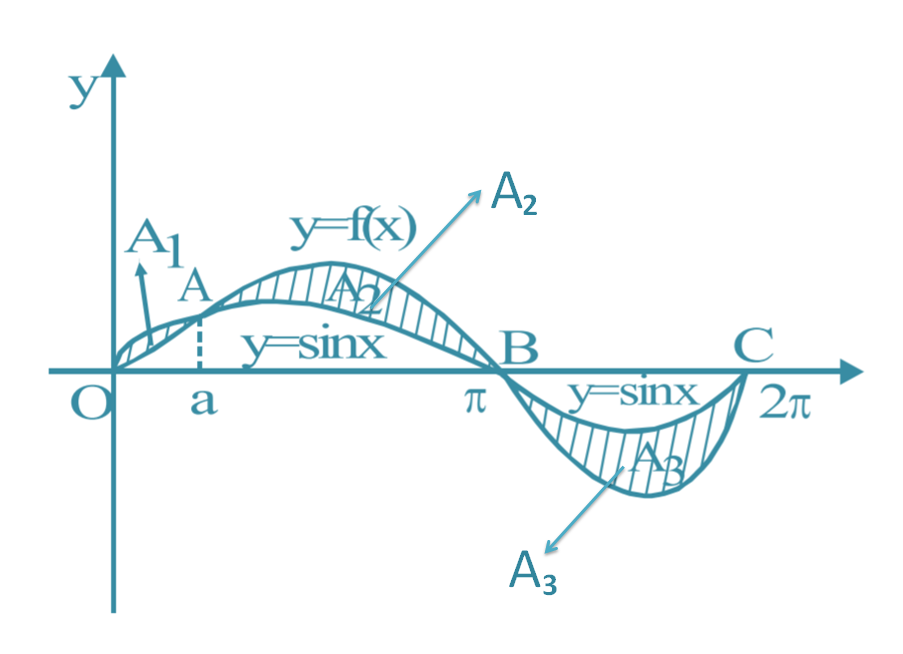
View SolutionIn the adjacent figure the graph of two function y=f(x) and y=sinx are given y=sin x intersects, y=f(x) at A(a,f(a)),B(π,0)andC(2π,0).
Ai(i=1,2,3) is the area bounded by the curves y=f(x)andy=sinx between x=0 and x=a,i=1 between x=a and x=π,i=2 between x=π and x=2π,i=3. If A1=1−sina+(a−1) cos a, determine the function f(x). Hence, determine a and A1. Also, calculate A2andA3.
 .
.
View SolutionDefine the function, f(x)=cos−1(cosx)−sin−1(sinx) in [0,2π] and find the area bounded by the graph of the function and the x-axis.
View SolutionConsider function f(x)=sin−1(sinx)+cos−1(cosx),x∈[0,2π]
(a) Draw the graph of y=f(x)
(b) Find the range of f(x)
(c) Find the area bounded by y=f(x) and x-axis
View SolutionThe area bounded by the graph of y=f(x),f(x)>0 on [0,a] and x-axis is a22+a2sina+π2cosa then find the value of f(π2).
View Solutionf(x)=max{sinx,cosx,12} the area of the region bounded by the curve y=f(x), X-axis Y-axis and x=2π is ……..Sq. units
View SolutionIf the area of the region bounded by the curve y=f(x), X - axis and x=1 and x=b is (b-1) sin (3b+4) f(x) ……
View Solutionदिए गये चित्र में दो फलन y=f(x) तथा y=sinx एक दुसरे को बिन्दु A(a,f(a)),B(π,0) तथा C(2π,0) पर काटते है | Ai(i=1,2,3) वक्र y=f(x) तथा y=sinx का x=0 तथा x=a के मध्य क्षेत्रफल, (i=1),x=a तथा x=π के मध्य, (i=2),x=π तथा x=2π के मध्य, (i=3) है| यदि Ai=1−sina+(a−1)cosa तो फलन f(x) ज्ञात कीजिए 'a',A1,A2 तथा A3 के मान ज्ञात कीजिए |
View Solution