Question

about to only mathematics

Answer

(0,0) or (0,5/2)

Explanation

A being on the y-axis may be chosen as (0,a). The diagonals intersect at P(1,2).

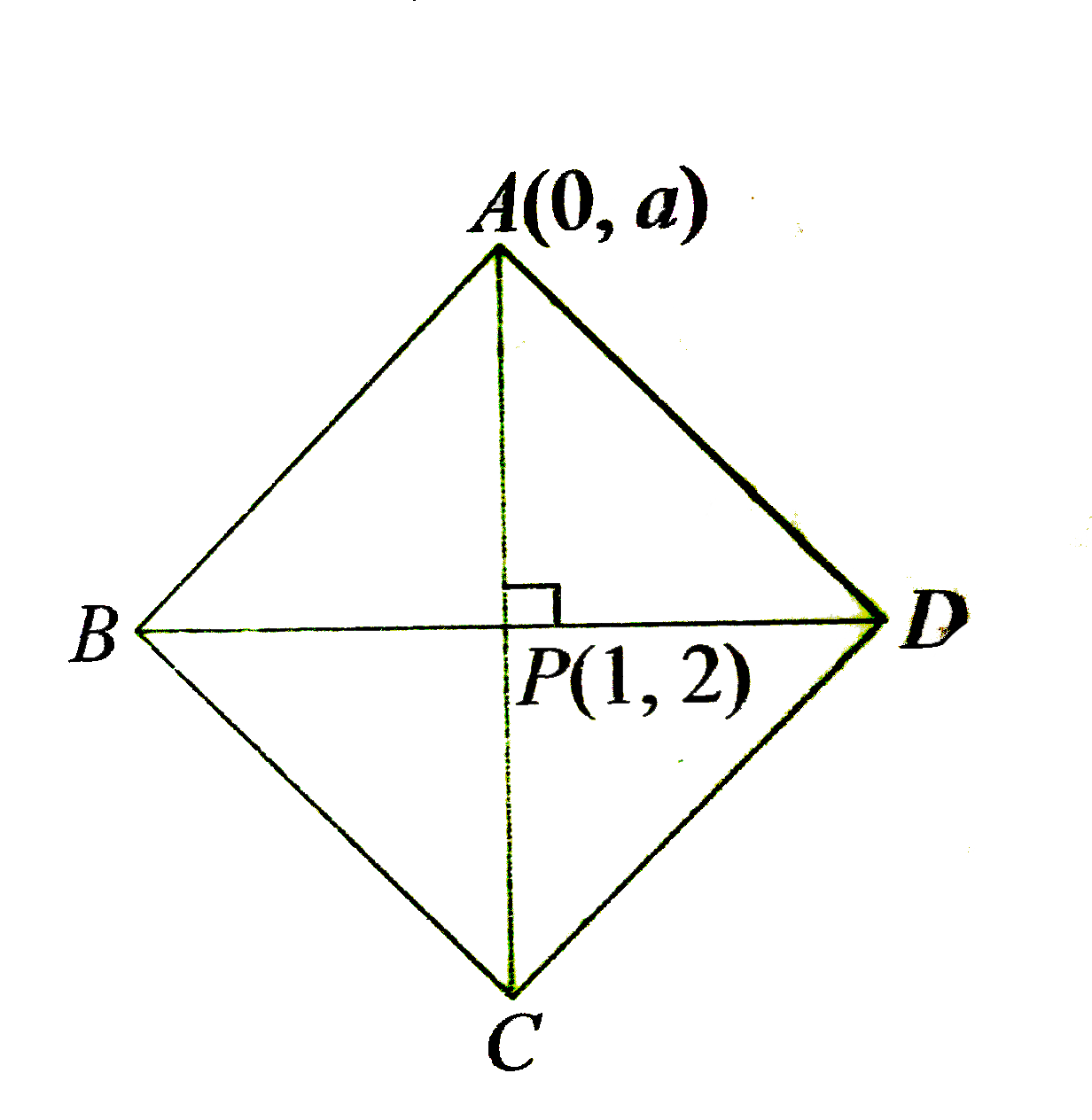
Again, we know that the diagonals will be parallel to the bisectors of the two given lines y=x+2 and y =7x+3, i.e.,
`(x-y+2)/(sqrt(2))= +-(7x-y+3)/(5sqrt(2))`
or 5x-5y+10 `=+-(7x-y+3)`
or 2x+4y-7=0 and 12x-6y+13=0
`therefore "Slope of diagonals are "m_(1) = -1//2 "and" m_(2) = 2`. Let diagonal `d_(1)` be parallel to 2x+4y-7 =0 and diagonal `d_(2)` be parallel to 12x-6y+13 = 0. The vertex A could be on any of the two diagonals. Hence, the slope of AP is either -1/2 or 2. Therefore,
`(2-a)/(1-0) = 2 or -(1)/(2)`
`i.e., a = 0 or (5)/(2)`
Hence, A is (0,0) or (0,5/2).