If a continous founction of defined on the real line R, assumes positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum values is negative, then the equation f(x)=0 has a root in R. Considetr f(x)=kex−x for all real x where k is real constant.
The line y=x meets y=kexfork≤0 at Solution in Tamil
1e
1
e
loge2
(a) kex−x=0 to have only one positive root means the line y=xk must be tangential to the curve y=ex.
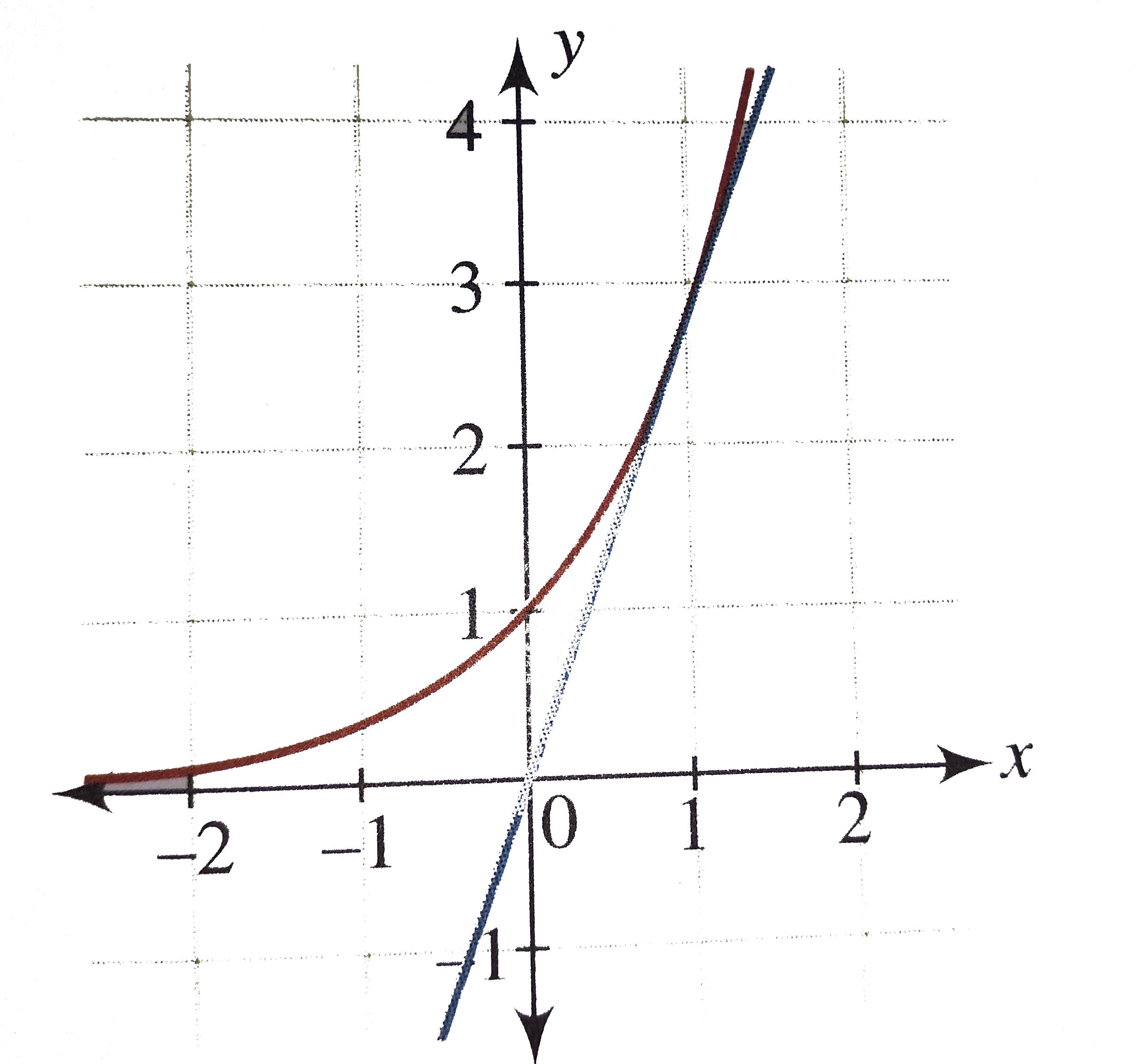
Let the line touch the curve at (x1,y1), then
(dydx)x1=ex1=1k
Also y1=ex1andy1=x−1k
⇒x1=1⇒k=1/e
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
03:06View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=002:13View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
06:07View SolutionIf a continuous function f defined on the real line R, assumes positive and negative values in R then the equation f(x)=0 has a root in R . For example, if it is known that a continuous function f on R is positive at some point and its minimum value is negative then the equation f(x)=0 has a root in R. Consider f(x)=kex−x for all real x where k is a real constant The line y=x meets y=kex for k≤0 at no point (b) one point two points (d) more than two points
03:01View SolutionIf a continuous function f defined on the real line R assume positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum value is negative, then the equation f(x)=0 has a root in R. Consider f(x)=kex−x, for all real x where k is a real constant.
The line y=x meets y=kex for k≤0 at03:23View Solutionf(x) is a polynomial function, f:R→R, such that f(2x)=f'(x)f''(x). Equation f(x) = x has (A) three real and positive roots (B) three real and negative roots (C) one real root (D) three real roots such that sum of roots is zero
04:35View SolutionIf a continous founction of defined on the real line R, assumes positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum values is negative, then the equation f(x)=0 has a root in R. Considetr f(x)=kex−x for all real x where k is real constant.
The positive value of k for which kex−x=0 has only root is05:59View SolutionIf a continous founction of defined on the real line R, assumes positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum values is negative, then the equation f(x)=0 has a root in R. Considetr f(x)=kex−x for all real x where k is real constant.
For k>0, the set of all values of k for which kex−x=0 has two distinct, roots, is05:59View Solutionयदि सतत् फलन f इस प्रकार है कि यह वास्तविक संख्या रेखा R पर धनात्मक और ऋणात्मक मान रखता है तब समीकरण f(x)=0 का एक मूल R में होगा। उदाहरण के लिए यदि यह ज्ञात हो कि सतत फलन f,R के कुछ बिंदुओं पर धनात्मक है तथा इसका न्यूनतम मान ऋणात्मक है तब समीकरण f(x)=0 का एक मूल R में होगा।
माना सभी वास्तविक x के लिए f(x)=kex−x है। जहां k एक वास्तविक नियतांक है।
k≤0 के लिए रेखा y=x,=kex−x से कितने बिंदुओं पर मिलती है।04:31View Solutionयदि सतत् फलन f इस प्रकार है कि यह वास्तविक संख्या रेखा R पर धनात्मक और ऋणात्मक मान रखता है तब समीकरण f(x)=0 का एक मूल R में होगा। उदाहरण के लिए यदि यह ज्ञात हो कि सतत फलन f,R के कुछ बिंदुओं पर धनात्मक है तथा इसका न्यूनतम मान ऋणात्मक है तब समीकरण f(x)=0 का एक मूल R में होगा।
माना सभी वास्तविक x के लिए f(x)=kex−x है। जहांँ k एक वास्तविक नियतांक है।
k का धनात्मक मान जिसके लिए kex−x=0 का केवल मूल है02:46View Solutionयदि सतत् फलन f इस प्रकार है कि यह वास्तविक संख्या रेखा R पर धनात्मक और ऋणात्मक मान रखता है तब समीकरण f(x)=0 का एक मूल R में होगा। उदाहरण के लिए यदि यह ज्ञात हो कि सतत फलन f,R के कुछ बिंदुओं पर धनात्मक है तथा इसका न्यूनतम मान ऋणात्मक है तब समीकरण f(x)=0 का एक मूल R में होगा।
माना सभी वास्तविक x के लिए f(x)=kex−x है। जहां k एक वास्तविक नियतांक है।
k का धनात्मक मान जिसके लिए kex−x=0 का केवल मूल है03:45View SolutionIf a continuous function f defined on the real line R assume positive and negative values in R, then the equation f(x)=0 has a root in R. For example, if it is known that a continuous function f on R is positive at some point and its minimum value is negative, then the equation f(x)=0 has a root in R. Consider f(x)=kex−x, for all real x where k is a real constant.
The positive value of k for which kex−x=0 has only one root is04:36View SolutionIf x and y are arbitrary extensive variables, then
05:32View Solutionअनुच्छेद : (प्र. 14 से 16)
यदि एक संतत् फलन f जो वास्तविक रेखा R पर परिभाषित है, R में धनात्मक तथा ऋणात्मक मान लेता है, तब समीकरण f(x)=0 का एक मूल R मे होगा। उदाहरण के लिए, यदि यह ज्ञात है की R के कुछ बिन्दुओं पर संतत् फलन f धनात्मक है तथा इसका न्यूनतम मान ऋणात्मक है, तब समीकरण f(x)=0 का एक मूल R में होगा।
माना f(x)=kex सभी वास्तविक x के लिए, जहाँ k एक वास्तविक अचर है।
रेखा y=x,y=kex को k≤0 के लिए निम्न बिन्दुओं पर मिलती है -12:55View Solutionअनुच्छेद : (प्र. 14 से 16)
यदि एक संतत् फलन f जो वास्तविक रेखा R पर परिभाषित है, R में धनात्मक तथा ऋणात्मक मान लेता है, तब समीकरण f(x)=0 का एक मूल R मे होगा। उदाहरण के लिए, यदि यह ज्ञात है की R के कुछ बिन्दुओं पर संतत् फलन f धनात्मक है तथा इसका न्यूनतम मान ऋणात्मक है, तब समीकरण f(x)=0 का एक मूल R में होगा।
माना f(x)=kex सभी वास्तविक x के लिए, जहाँ k एक वास्तविक अचर है।
k का धनात्मक मान जिसके लिए kex−x=0 का केवल मूल है, होगा -04:54View Solutionअनुच्छेद : (प्र. 14 से 16)
यदि एक संतत् फलन f जो वास्तविक रेखा R पर परिभाषित है, R में धनात्मक तथा ऋणात्मक मान लेता है, तब समीकरण f(x)=0 का एक मूल R मे होगा। उदाहरण के लिए, यदि यह ज्ञात है की R के कुछ बिन्दुओं पर संतत् फलन f धनात्मक है तथा इसका न्यूनतम मान ऋणात्मक है, तब समीकरण f(x)=0 का एक मूल R में होगा।
माना f(x)=kex सभी वास्तविक x के लिए, जहाँ k एक वास्तविक अचर है।
k>0 के लिए, k के सभी मानों का समुच्चय जिसके लिए kex−x=0 के दो भिन्ना मूल होंगे, है-05:33View Solution