Letf(x)={x3+x2+3x+sinx∣(3+s∈1x,),x≠0.0x=0 then the number of point where f(x) attains its minimum value is_____Solution in Tamil
f(x)=⎧⎪
⎪⎨⎪
⎪⎩b−ax−cx,x<0b−ax+cx,0≤x<baax−b+cx,x≥ba
=⎧⎪
⎪⎨⎪
⎪⎩b−(a+c)x,x<0b+(c−a)x,0≤x<ba(a+c)x−b,x≥ba
The graphs of the function for different situations are as shown in the following figures.
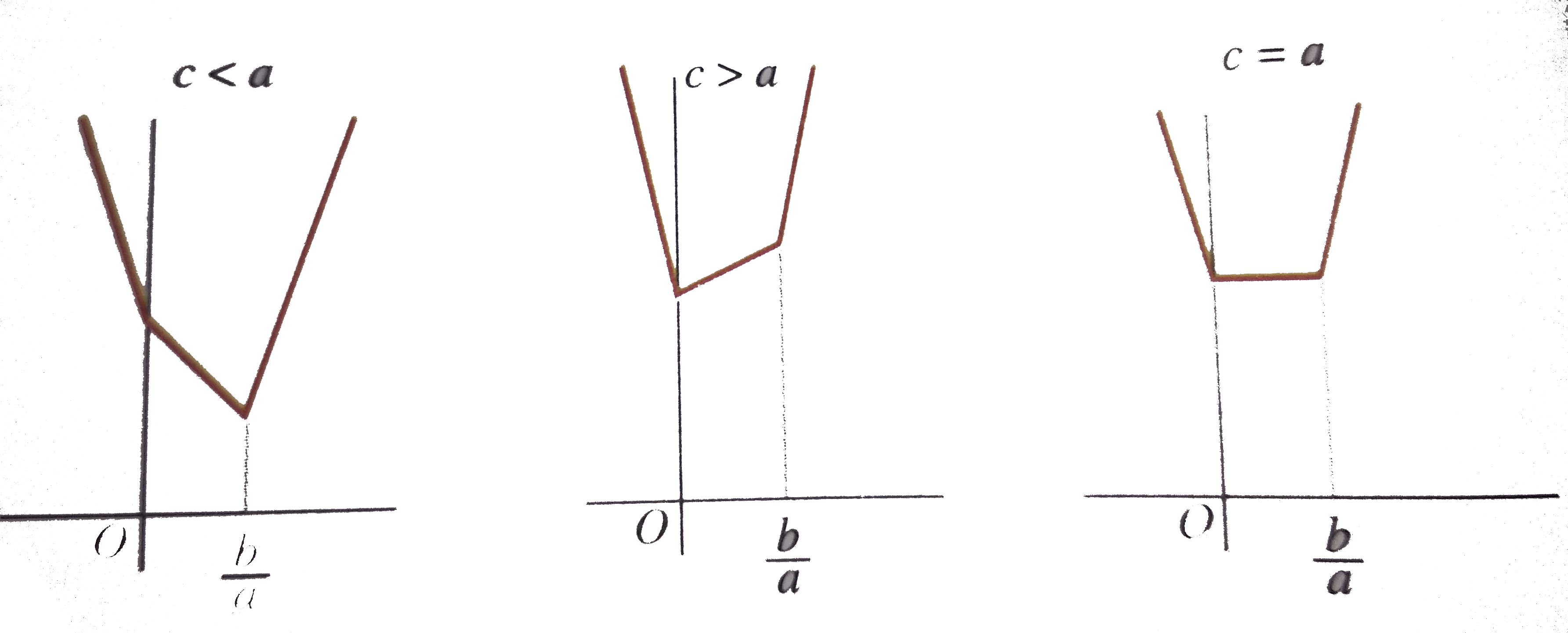
From the figure, we can see that for c<aandc>a, there is only point of minima.
For c=a, there are infinite points of minima.
Thus, for exactly one point of minima, c≠a.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLetf(x)={∣∣x2−3x∣∣+a,0≤x<32−2x+3,x≥32 If f(x) has a local maxima at x=32 , then greatest value of |4a| is _________
View SolutionLetf(x)={xeax,x≤0x+ax2−x3,x>0 where a is a positive constant. Find the interval in which f′(x) is increasing.
View SolutionLetf(x)={x3+x2+3x+sinx∣(3+s∈1x,),x≠0.0x=0 then the number of point where f(x) attains its minimum value is_____
View SolutionL e tf(x)=x^3-x^2+12 x-3x=2,f(x)h a s 2ans1. Let f(x)=x-x+12x-3 thenx=2, f(x) has1) a maximum 2) a minimum3) both a maximum and a minimum4 neither a maximum nor a minimum
View SolutionIf quad {x^(3),x<0 and 0x=0 and -x^(3),x<0 then f is derivable at x=0 and -x^(3),x<0
View Solutionf(x)={e^(-(1)/(x^(2)))x>0 and 0x<=0 then f(x) is
View SolutionLet f(x)=⎧⎨⎩∣∣x3+x2+3x+sinx(3+sin(1)x)x≠00x=0
Then the number of points where f(X) attians its minimum value is _______.
View SolutionIf f(x)=ex−esinx2(xsinx),x≠0 is continuous at x = 0, then f(0) =
View SolutionLetf(x)={∣∣x2−3x∣∣+a,0≤x<32−2x+3,x≥32 If f(x) has a local maxima at x=32 , then greatest value of |4a| is _________
View SolutionLetf(x)={∣∣x3+x2+3x+sinx∣∣(3+sin(1x))x≠00x=0 then the number of point where f(x) attains its minimum value is_____
View SolutionLetf(x)={∣∣x2−3x∣∣+a,0≤x<32−2x+3,x≥32 If f(x) has a local maxima at x=32 , then greatest value of |4a| is _________
View Solutionagreed f(x)={(|x^(3)+x^(2)+3x+sinx|(3+"sin"1/x),x!=0),(0,x=0):} Then the number of points for which f (x) has a lower value is
View SolutionIf f(x) = (e^(x)-e^(sinx))/(2(x sinx)) , x != 0 is continuous at x = 0, then f(0) =
View Solution
