Draw the graph of the function f(x)=x−∣∣x−x2∣∣,−1≤x≤1 and find the points of non-differentiability. Solution in Tamil
We have y=f(x)=x−∣∣x−x2∣∣
={x−(x2−x),x2−x≥0x−(x−x2),x2−x<0
={x−(2x−x2),x≤0orx≥1x2,0<x<1
The graph of the function y=2x−x2=x(2−x) is a downward parabola intersecting the x-axis at x=0andx=2.
Thus, the graph of the function y=f(x) is as follows:
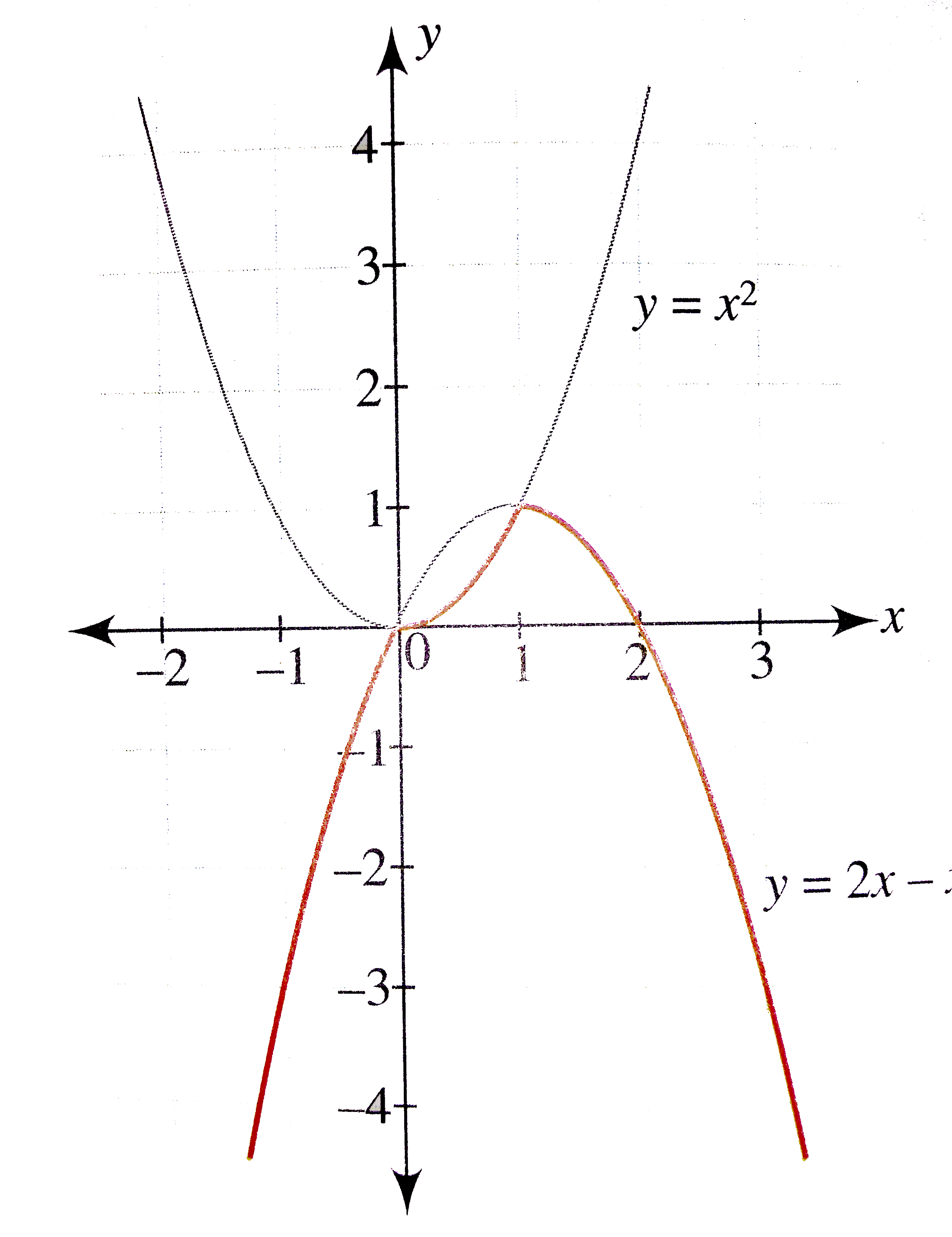
Clearly from the graph the function is continuous but non-differentiable at x=0,1.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionDraw the graph of the function f(x)=x−∣∣x−x2∣∣,−1≤x≤1 and find the points of non-differentiability.
View SolutionDraw the graph of the function f(x)=∣∣∣(x+12)[x]∣∣∣,−2≤x≤2, where [⋅] denotes the greatest integer function. Find the points of discontinuity and non-differentiability.
View Solutionफलन :
f(x)=⎧⎪⎨⎪⎩(1−x)x<1(1−x)(2−x)1≤x≤2(3−x)x>2
की बिंदु x=1 पर अवकलनीयता की जाँच कीजिए।
View SolutionDraw the graph of the function and discuss the continuity and differentiability at x = 1 for, f(x)={3x,when−1≤x≤14−x,when1<x<4
View SolutionDraw the graph of the function f(x)=x−∣∣x−x2∣∣,−1≤x≤1 and discuss the continuity or discontinuity of f in the interval −1≤x≤1
View SolutionConsider a function defined in [−2,2]
f(x)=⎧⎪⎨⎪⎩{x}−2≤x<−1|sgnx|−1≤x≤1{−x}1<x≤2, where {.} denotes the fractional part function.
The number of points for x∈[−2,2] where f(x) is non-differentiable is:
View Solutiony=[x]+|1−x|,−1≤x≤3 का लेखाचित्र बनाइए | वह बिंदु, जहाँ यह फलन अवकलनीय नहीं है, यदि है, तो ज्ञात कीजिए |
View SolutionDraw the graph of the function: f(x)=|1−x|+|1+x|,−2≤x≤2
View SolutionDraw the graph of the function f(x)={1+x−1≤x≤01−x0<x≤1
View SolutionDraw the graph of the function f(x)=x−∣∣x−x2∣∣,−1≤x≤1 and find the points of non-differentiability.
View SolutionDraw the graph of the function f(x)=x−|x2−x|−1≤x≤1, where [⋅] denotes the greatest integer function. Find the points of discontinuity and non-differentiability.
View Solutionफलन f(x)=x−∣∣x−x2∣∣,−1≤x≤1 का आरेख बनाईये तथा अंतराल −1≤x≤1 में f की संतत्ता व असंतत्ता की विवेचना कीजिए।
View Solution
