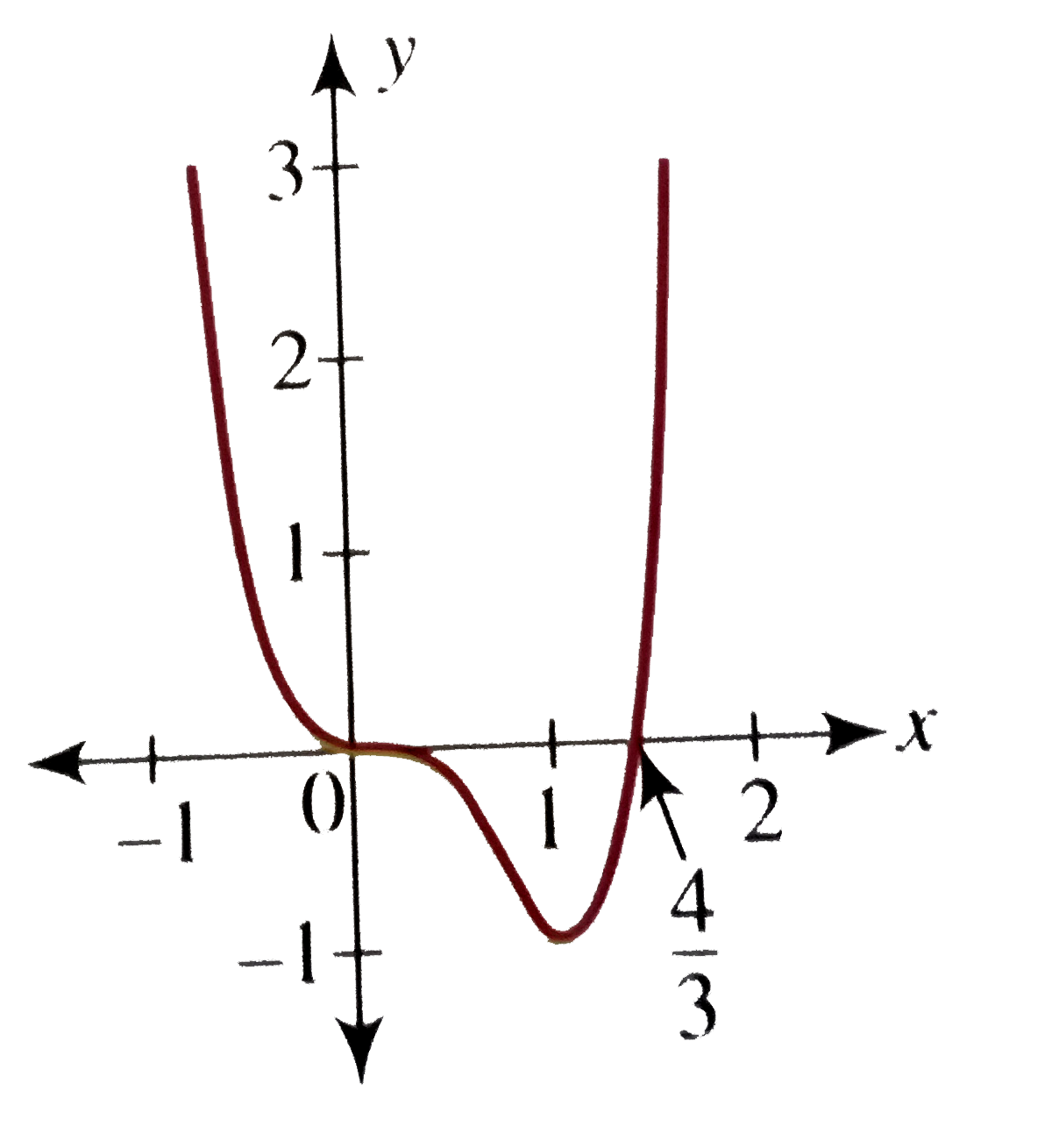
Draw the graph of the function y=3x4−4x3. Discuss the points of local extremum, inflection and intervals of monotonicity.Solution in Tamil
We have y=f(x)=3x4−4x3=x3(3x−4)
The sign scheme of y=f(x) is as follows.
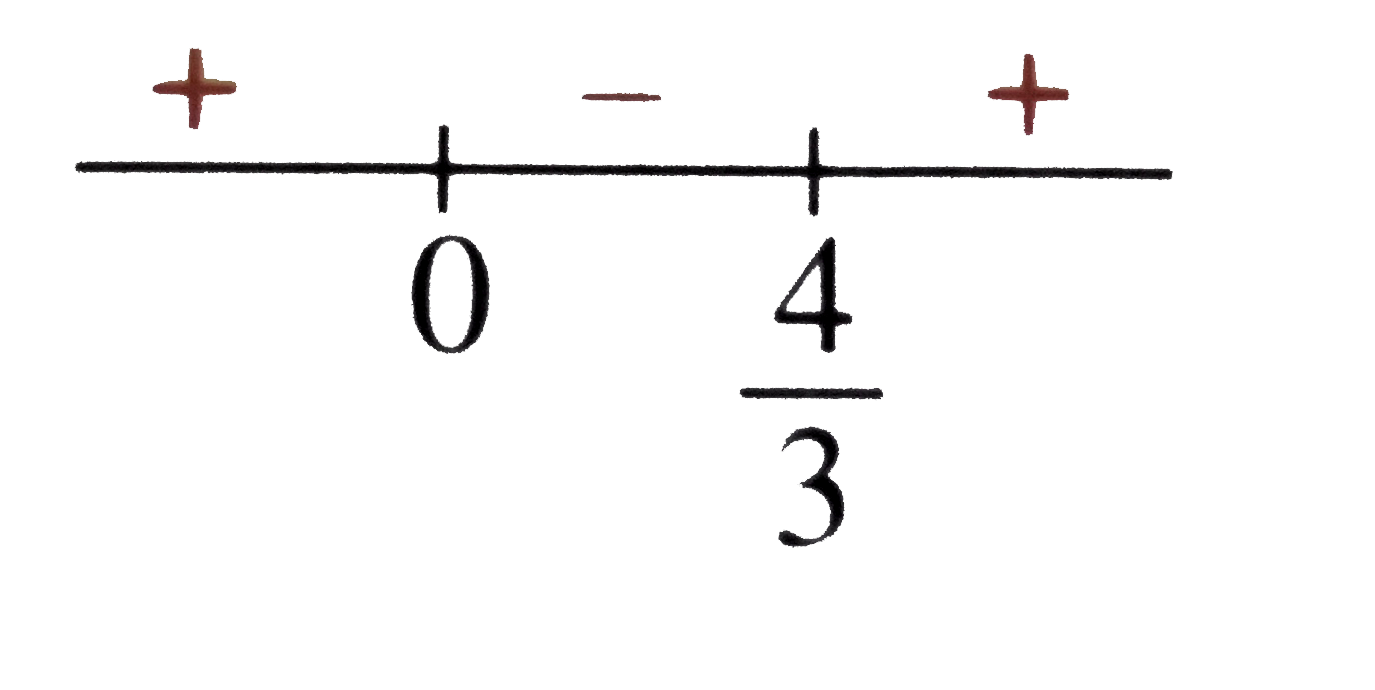
(3x−4)→ Graph crosses the x-axis at x=4/3 without touching the x-axis.
x2→ Graph crosses the x-axis at (0,0) and also touches the x-axis at this point.
f'(x)=12x3−12x2
=12x2(x−1)
f'(x)=0
∴ x=0,1
f'(x)<0,if x<1, where f(x) decreases
f'(x)>0,if x>1, where f(x) increases
x=1 is the point of minima.
Also f''(x)=36x2−24x=12x(3x−2)
f''(x)=0,if x=0,2/3, which are points of inflection .
The graph of the function is as shown in the following figure.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise14videos
GRAPHICAL TRANSFORMATIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
Similar Questions
Draw the graph of y=(x−1)(x2−x+1).
03:11View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=006:31View SolutionDraw the graph of y=tan−1x−cot−1x.
09:40View SolutionDraw the graph of y=1(1/x).
04:53View SolutionDraw the graph of the function y=3x4−4x3. Discuss the points of local extremum, inflection and intervals of monotonicity.
05:02View SolutionDraw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
05:41View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=2x3+3x2−12x14:21View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=xx−511:43View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=ex1−ex03:18View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=x33−logx07:08View SolutionFind the intervals of monotonicities and hence find the local extremum for the following functions:
f(x)=sinxcosx+5,x∈(0,2π)04:19View SolutionFor the function f(x)=4x3+3x2−6x+1 find the intervals of monotonicity, local extrema, intervals of concavity and points of inflection.
01:07:57View SolutionDraw the graph of the function y=3x4−4x3. Discuss the points of local extremum, inflection and intervals of monotonicity.
01:03:29View SolutionDraw the graph of f(x)=2x+3x2/3 and discuss the type of non-differentiability for the function. Also find the point of inflection.
01:09:21View SolutionFind the intervals in which the graphs of the following functions are concave or convex and locate the points of inflection :
y=3x4−8x3+6x2+1201:07:57View SolutionTheory OF Monotonicity || Local Extremum Points
01:03:29View Solution
