A parallelepiped $S$ has base points $A, B, C a n d D$ and upper face points $A^{'}, B^{'}, C^{'}, a n d D'$ . The parallelepiped is compressed by upper face $A' B' C' D'$ to form a new parallepiped $T$ having upper face points $A,B, C a n dD$ . The volume of parallelepiped $T$ is 90 percent of the volume of parallelepiped $S .$ Prove that the locus of $A$ is a plane.Solution in Tamil

Video Solution

Text Solution

Verified by Experts

S is the parallelepiped with base point $A, B, C and D$ and upper face points $A', B', C' and D'$ . Let its volume ve $V_{s}$ . By compressing it by upper face $A', B', C' and D'$ , a new parallelepiped T is formed whose upper face points are now $A'', B'', C'' and D''$ . Let its volume be $V_{T}$ .
Let $h$ be the height of original parallelepiped S. Then
$V_{S} = (area of A B C D) \times h$ (i)
Let equation of plane $A B C D$ be $a x + b y + c z + d = 0 and A'' (α, β, γ)$ .

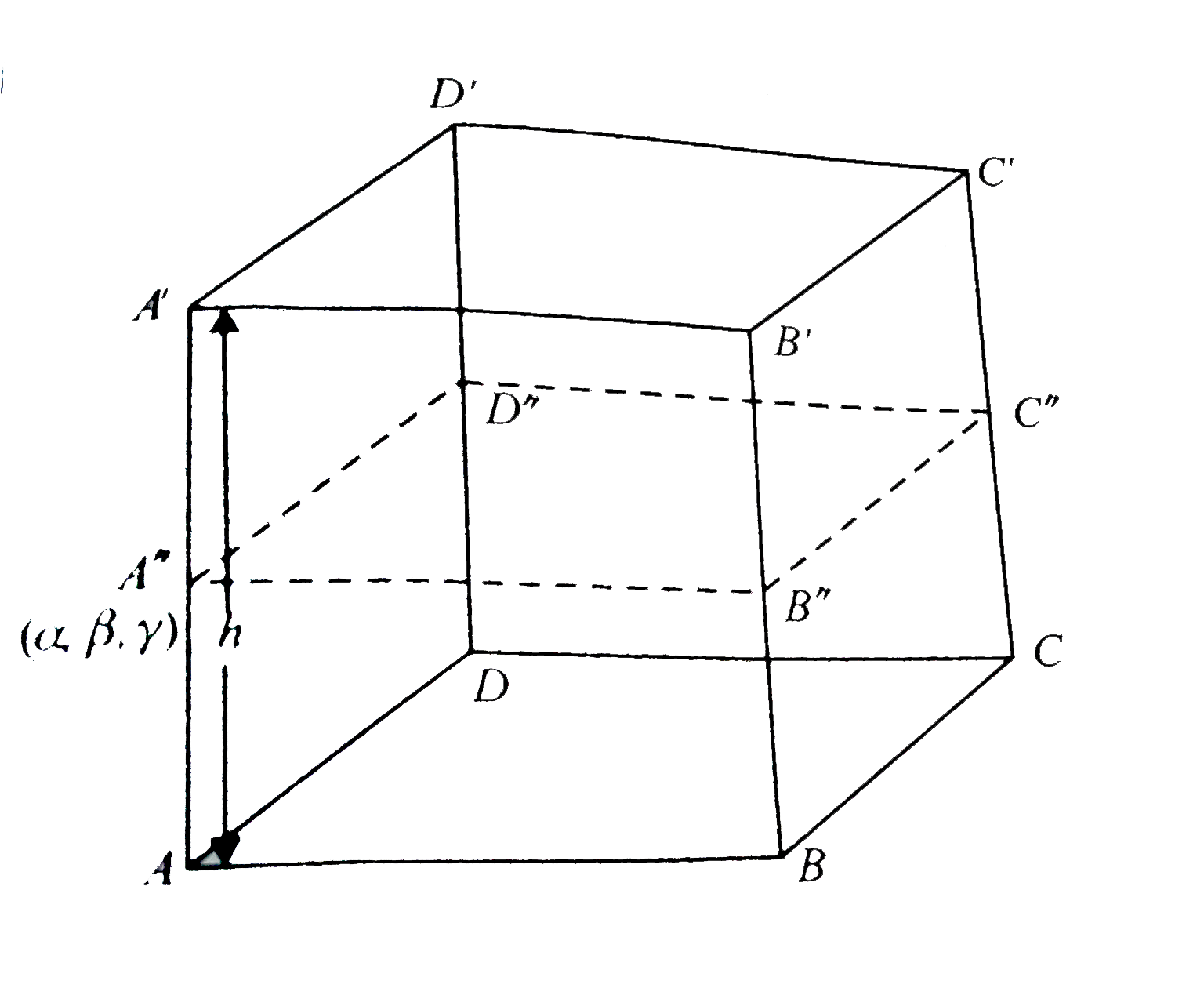
Then the height of the new parallelepiped T is the length of the perpendicular from $A''$ to $A B C D$ , i.e., $\frac{a α + η + c γ + d}{\sqrt{a^{2} + b^{2} + c^{2}}}$ . Therefore
$V_{T} = (ar A B C D) \times \frac{(a α + η + c γ + d)}{\sqrt{a^{2} + b^{2} + c^{2}}}$ (ii)
But given that $V_{T} = \frac{90}{100} V_{s}$ (iii)
From (i), (ii) and (iii), we get
$\frac{a α + η + c γ + d}{\sqrt{a^{2} + b^{2} + c^{2}} = 0.9 h}$
or $a α + η + c γ + d - 0.9 h \sqrt{a^{2} + b^{2} + c^{2}} = 0$
Therefore, the locus of $A'' (α, β, γ)$ is $a x + b y + c z + d - 0.9 h \sqrt{a^{2} + b^{2} + c^{2}} = 0$ , which is a plane parallel to $A B C D$ . Hence proved.

Updated on:21/07/2023

|

Class 12 MATHS THREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions

CENGAGE-THREE-DIMENSIONAL GEOMETRY -JEE Previous Year

Home
Ask Doubt
Profile