Question

$A$ is a set containing $n$ different elements. A subset $P$ of $A$ is chosen. The set $A$ is reconstructed by replacing the elements of $P$. A subset $Q$ of $A$ is again chosen. The number of ways of choosing $P$ and $Q$
so that $P\cap Q$ contains exactly two elements is
(a). ${.}^n{C}_3\times 2^n$
(b). ${.}^n{C}_2\times 3^{n-2}$
(c). $3^{n-1}$
(d). none of these

Options

A. `(3^(n-m))/(4^(n))`
B. `(.^(n)C_(m).3^(m))/(4^(n))`
C. `(.^(n)C_(m).3^(n-m))/(4^(n))`
D. none of these

Answer

C

Explanation

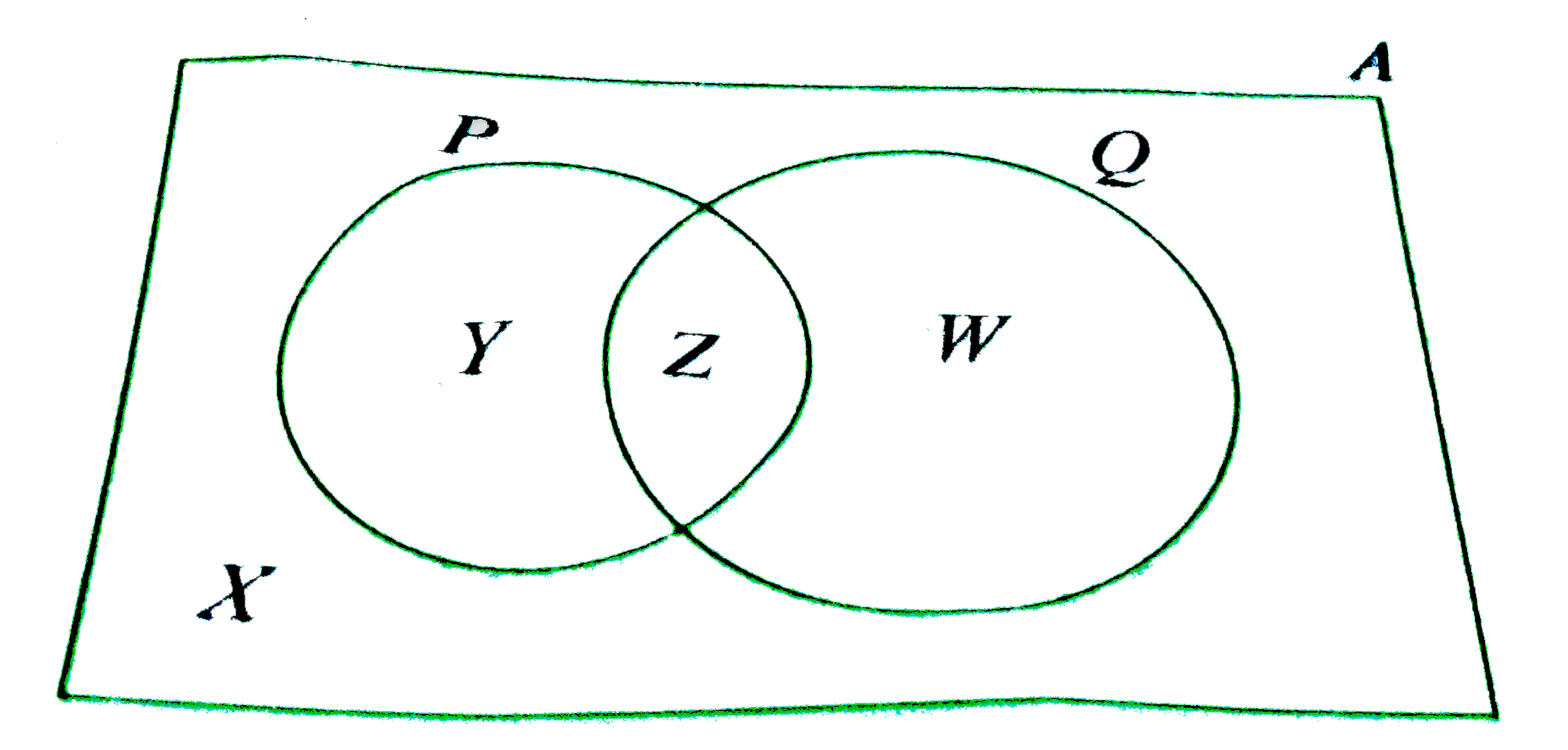
Sets P and Q are subsets of set A. Sets P and Q are dividing set A in four regions X, Y, Z and W.
`therefore` Total number of cases
= Number of ways in which n elements can be distributed in four regions = `4^(n)`
If set `(P nn Q)` has exactly m elements, we can select these m elements in `.^(n)C_(m)` ways. Remaining n - m elements can be distributed in the regions X, Y and W in `3^(n-m)` ways.
`therefore` Number of favourable ways = `.^(n)C_(m) xx 3^(n-m)`
`therefore` Required probability = `(.^(n)C_(m) xx 3^(n-m))/(4^(n))`