A proton strikes another proton at rest with speed vα. Assume impact parameter to be zero. Their closest distance of approach is (mass of proton is m)
e22πεmv20
e2πε0mv20
e2mv20
Zero
To find the closest distance of approach between two protons, we can use the principle of conservation of energy. Here’s a step-by-step solution to the problem:
Step 1: Identify the Initial Conditions
- One proton is at rest, and the other proton is moving with speed vα.
- The mass of each proton is m.
Step 2: Calculate Initial Kinetic Energy
The initial kinetic energy (KE) of the moving proton can be calculated using the formula:
KEinitial=12mv2α
Step 3: Identify Potential Energy at Closest Approach
When the two protons are at their closest distance of approach d, all the kinetic energy will be converted into potential energy (PE) due to the electrostatic repulsion between them. The potential energy at this distance is given by:
PE=k⋅q1⋅q2d
where k=14πϵ0 and q1=q2=e (the charge of a proton).
Thus, the potential energy can be expressed as:
PE=14πϵ0⋅e2d
Step 4: Apply Conservation of Energy
According to the conservation of energy, the initial kinetic energy equals the potential energy at the closest distance of approach:
12mv2α=14πϵ0⋅e2d
Step 5: Rearranging the Equation to Solve for d
Rearranging the equation to solve for d:
d=14πϵ0⋅e212mv2α
This simplifies to:
d=2e24πϵ0mv2α
d=e22πϵ0mv2α
Final Answer
Thus, the closest distance of approach d is given by:
d=e22πϵ0mv2α
---
- One proton is at rest, and the other proton is moving with speed vα.
- The mass of each proton is m.
The initial kinetic energy (KE) of the moving proton can be calculated using the formula:
KEinitial=12mv2α
When the two protons are at their closest distance of approach d, all the kinetic energy will be converted into potential energy (PE) due to the electrostatic repulsion between them. The potential energy at this distance is given by:
PE=k⋅q1⋅q2d
where k=14πϵ0 and q1=q2=e (the charge of a proton).
PE=14πϵ0⋅e2d
According to the conservation of energy, the initial kinetic energy equals the potential energy at the closest distance of approach:
12mv2α=14πϵ0⋅e2d
Rearranging the equation to solve for d:
d=14πϵ0⋅e212mv2α
This simplifies to:
d=2e24πϵ0mv2α
d=e22πϵ0mv2α
Thus, the closest distance of approach d is given by:
d=e22πϵ0mv2α
Topper's Solved these Questions
- ATOMS AND NUCLEI BOOK - PHYSICS WALLAHCHAPTER - ATOMS AND NUCLEI EXERCISE - LEVEL-2
30 Videos
- ATOMS AND NUCLEI BOOK - PHYSICS WALLAHCHAPTER - ATOMS AND NUCLEI EXERCISE - NEET PAST 5 YEARS QUESTIONS
20 Videos
- AMINES BOOK - PHYSICS WALLAHCHAPTER - AMINES EXERCISE - NEET Past 5 Years Questions
11 Videos
- BIOMOLECULESBOOK - PHYSICS WALLAHCHAPTER - BIOMOLECULESEXERCISE - NEET PAST 5 YEARS QUESTIONS
13 Videos
Similar Questions
Write the relation for (i) the distance of closest approach and (ii) impact parameter.
View SolutionAn α-particle accelerated through V volt is fired towards a nucleus . Its distance of closest approach is r. If a proton acceleration throught the same potential is fired towards the same nucleus, the distance of closest approach of proton will be xr. Find value of x.
View Solution
Knowledge Check
A proton of mass m moving with a speed v0 apporoches a stationary proton that is free to move. Assuming impact parameter to be zero., i.e., head-on collision. How close will be incident proton go to other proton ?
Ae3πε0m2v0Be3πε0mv0Ce2πε0mv20DNone of theseWhich of the following masses is closest to the mass of a proton ?
A10−27 kgB10−31 kgC10−19 kgD10−15 kgA proton with kinetic energy K, strikes another proton at rest. If the collision is head-on, find the correct graph between K and the distance of closest approach, r.
A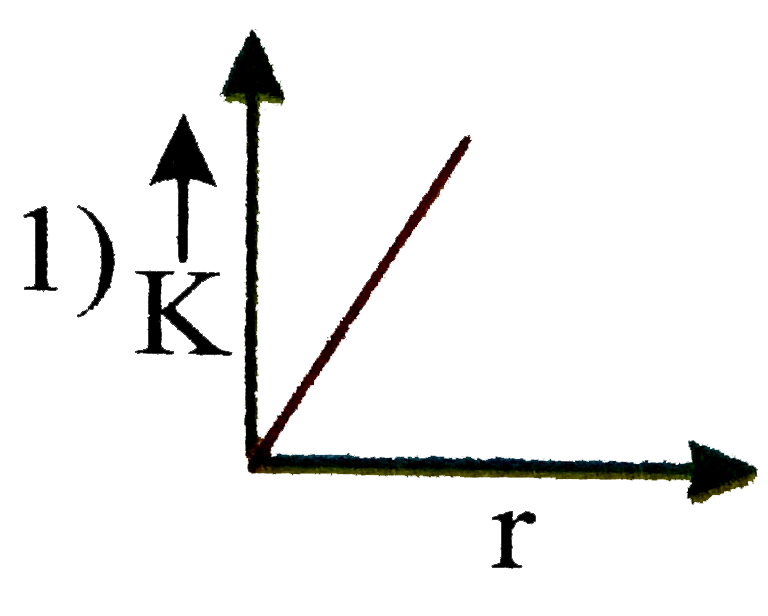 B
B C
C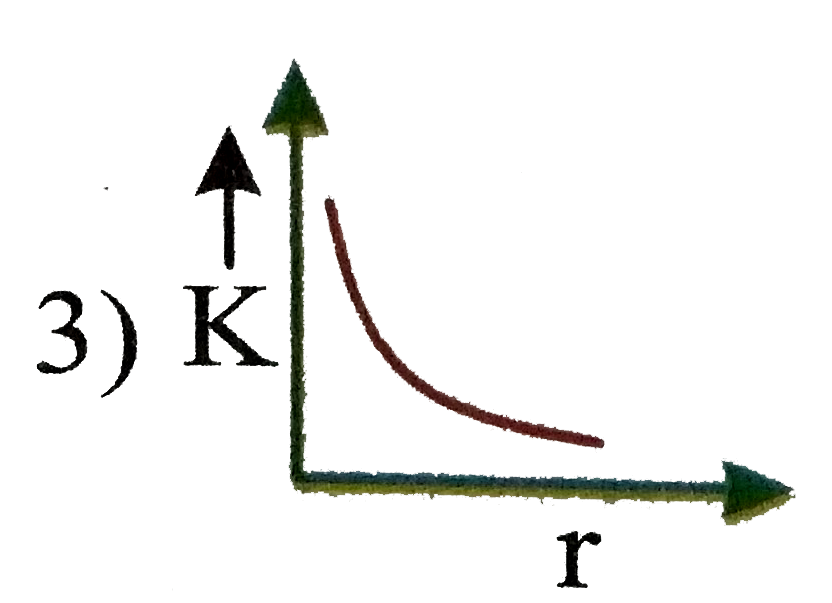 D
D
A proton moves from a large distance with a speed u m/s directly towards a free proton originally at rest. Find the distance of closest of closest approach for the two protons in terms of mass of proton m and its charge e.
View SolutionA proton moves from a large distance with a speed u m/s directly towards a free proton originally at rest. Find the distance of closest of closest approach for the two protons in terms of mass of proton m and its charge e.
View SolutionAn alpha-particle accelerated through V volt is fired towards a nucleus . Lts distance of closest approach is r.lf a proton accelerated through the same potential is fired towards the same nucleus, then distance of closest approach of proton will be
View SolutionAn α− paticle approaches the target nucleus of copper (Z = 29) is such a way that the vlaue of impact parameter is zero. The distance of closest approach will be
View SolutionAn α-particle accelerated through V volt is fired towards a nucleus . Its distance of closest approach is r . If a proton accelerated through the same potential is fired towards the same nucleus , the distance of closest approach of the proton will be :
View Solution
