दिए गए चित्र में D भुजा BC का मध्य बिंदु है और AE⊥BC यदि BC = a, AC = b, AB = C, ED = x, AD = P और AE = h तो सिद्ध करें कि : b2=P2+ax+a24
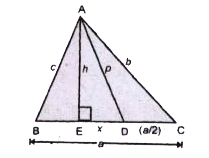
The correct Answer is:b2=p2+ax+a24
Step by step video, text & image solution for दिए गए चित्र में D भुजा BC का मध्य बिंदु है और AE bot BC यदि BC = a, AC = b, AB = C, ED = x, AD = P और AE = h तो सिद्ध करें कि : b^(2) = P^(2) + ax + (a^(2))/(4) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- त्रिभुज BOOK - KIRAN PUBLICATIONCHAPTER - त्रिभुज EXERCISE - लघु उत्तरीय प्रश्न
16 Videos
- त्रिभुज BOOK - KIRAN PUBLICATIONCHAPTER - त्रिभुज EXERCISE - लघु उत्तरीय प्रश्न (रिक्त स्थानों को भरे :- )
4 Videos
- त्रिभुज BOOK - KIRAN PUBLICATIONCHAPTER - त्रिभुज EXERCISE - EXERCISE - 6.4
17 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KIRAN PUBLICATIONCHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - Exercise 8.4 (वस्तुनिष्ट प्रश्न)
19 Videos
- दो चर वाले रैखिक समीकरण युग्म BOOK - KIRAN PUBLICATIONCHAPTER - दो चर वाले रैखिक समीकरण युग्म EXERCISE - वस्तुनिष्ट प्रश्न
12 Videos
Similar Questions
दिए गए चित्र में DE ∣∣ BC तथा ADDB=35 है। यदि AC = 4.8 सेमी. हो, तो AE की लम्बाई ज्ञात करें।
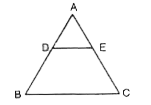
View Solutionरिक्त स्थानों को भरें :
(i) दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात उनकी संगत भुजाओं के .......... के अनुपात के बराबर होता है ।
View Solutionदो समरूप त्रिभुजों ABC और DEF में AC=3cm और DF=5cm दोनों त्रिभुजों के क्षेत्रफलों का अनुपात ज्ञात कीजिए ।
View Solution9sec2A−9tan2A बराबर है
View Solutionयदि a1a2≠b1b2 तब समीकरण निकाय a1x+b1y+c1=0 और a2x+b2y+c2=0 के कितने हल हैं?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionIn the following figure, if the tension in the string AB is 51N, then the tension in the string BC will be :- ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R03_E05_005_Q01.png" width="80%"gt
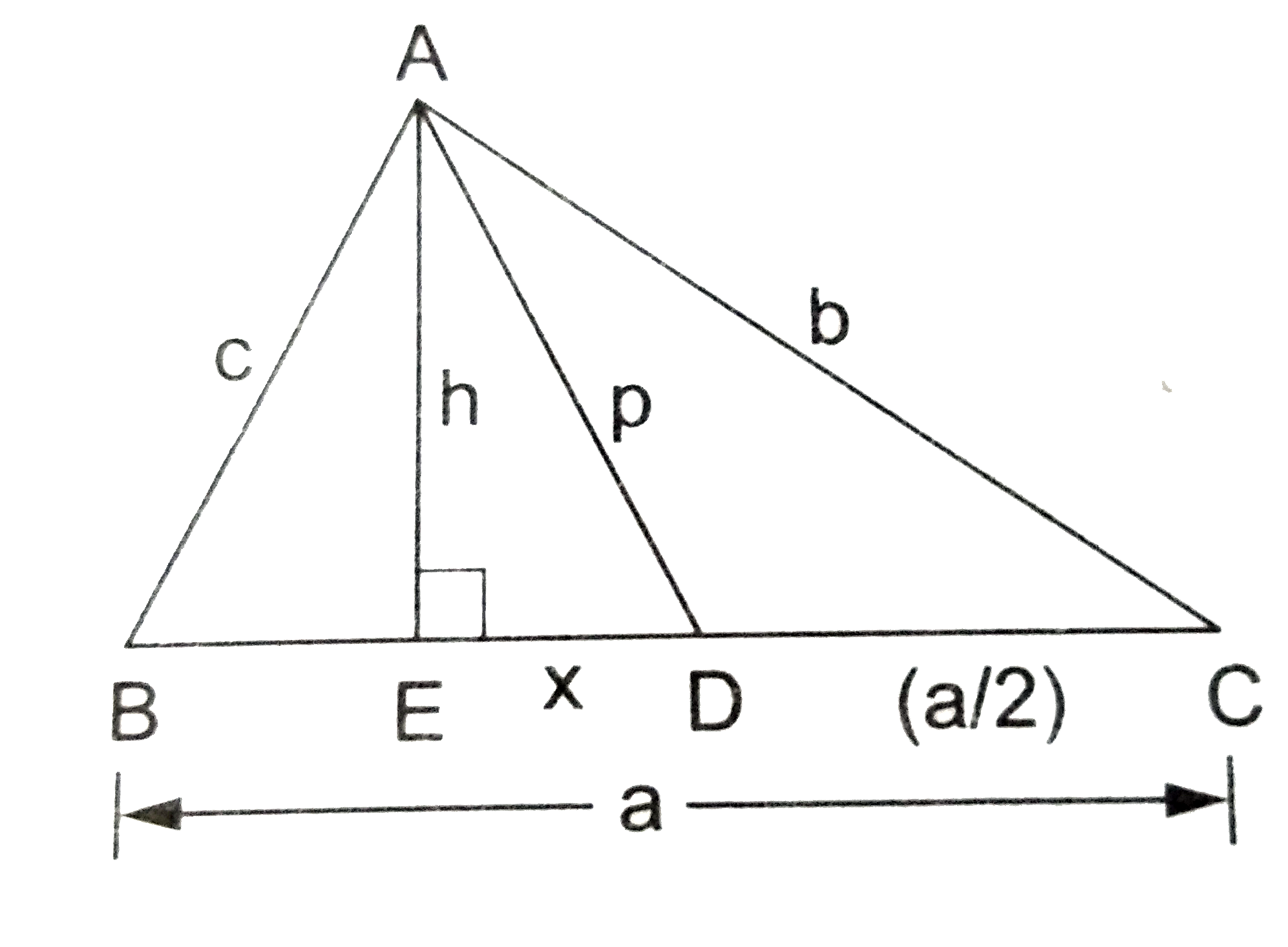
View SolutionIn the given figure, D is the midpoint of side BC and AE⊥BC. If BC=a,AC=b,AB=c,ED=xAD=pandAE=h prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii) (b2+c2)=2p2+12a2
(iv)(b2−c2)=2ax.
View SolutionD is the mid point of side BC and AE⊥BC. If BC=a, AC= b, AB=c, ED=x, AD=p and AE=h, prove that
(i)b2=p2+ax+a24
(ii) c2=p2−ax+a24
(iii)b2+c2=2p2+a22
View SolutionBC யின் மையப்புள்ளி D மற்றும் AE ⊥BC BC =a ,AC =b ,AB =c ED =x ,AD =p மற்றும் AE =h எனில் b2=p2 +ax+ a24 என நிரூபிக்க ?
View SolutionBC யின் மையப்புள்ளி D மற்றும் AE ⊥BC BC =a ,AC =b ,AB =c ED =x ,AD =p மற்றும் AE =h எனில் c2=p2_ax+a24 என நிரூபிக்க ?
View Solution
