Calculate the area of the region enclosed between the circles : and (using integration)Solution in Punjabi
Step by step video solution for Calculate the area of the region enclosed between the circles : x^2 + y^2 = 4 and (x - 2)^2 + y^2 = 4 (using integration) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the area of the region bounded by the curve y=x, and the lines x=1,x=4 and the x-axis.
View SolutionFind the rate of change of the area of a circle with respect to its radius r whenr=3cm
View SolutionUsing integration, find the area of the region enclosed between the circles x2+y2=1 and (x−1)2+y2=1
View SolutionFind the area of the region bounded by the curves x2+y2=4 and (x−2)2+y2=4.
View Solutionसमाकलन के प्रयोग से वक्रो {(x,y):x29+y24≤1≤x3+y2} से घिरे क्षेत्र का क्षेत्रफल ज्ञात कीजिए।
View SolutionUsing the method of integration, find the smaller area enclosed by the circle x2+y2=4 and the line x+y=2.
View SolutionUsing integration ,find the area of the region enclosed between the circles x2+y2=4and (x−2)2+y2=4
View SolutionFind the area enclosed between the circles x2+y2=4 and (x−2)2+y2=4.
View SolutionFind the area of the region enclosed between the two circle x2+y2=4 and (x−2)2+y2=4.
View SolutionFind the area of the region enclosed between the two circle x2+y2=4 and (x−2)2+y2=4.
View SolutionUsing integration, find the area of the region enclosed between the two circles x2+y2=4 and (x−2)2+y2=4.
View SolutionA point chanrge of magnitude q=4.5nC is moving with speed v=3.6×107ms−1 parallel to the x-axis along the line y=3m. Find the magnetic field at the origin produced by this charge when the charge is at the point x=−4m, y=3m, as shown in Fig.

View SolutionFind the area of the region enclosed between the circles x2+y2=4 and (x−2)2+y2=4
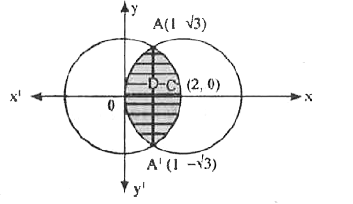
View SolutionFind the area of the region enclosed between the two circle x2+y2=4 and (x−2)2+y2=4.
View SolutionCalculate the area of the region enclosed between the circles : x2+y2=1 and (x−1)2+y2=1 (using integration)
View SolutionCalculate the area of the region enclosed between the circles : x2+y2=4 and (x−2)2+y2=4 (using integration)
View Solution
