Find which of the operations given above has identity.
(i) IN Q a * b a-b
Let a, b ∈ Q
∴ a*b =a - b ∈ b - a ∈ b*a
⇒ Operation * is not commutatve.
∴ a*(b*c) = a-(b-c)
=a-b + c
and (a*b) * c = (a-b) *c
= a-b-c
∴ a* (b*c) ≠ (a*b) * c
Therefore, operation * is not associative.
(ii) In Q a*b =a2+b2
Let a,b ∈ Q
∴ a* b =a2+b2
=b2+a2= b*a
⇒ Operation * is commutative.
Let a,b,c ∈ Q
∴ a*(b*c) = a*(b2+c2)
=a2+(b2+c2)2
and (a*b)*c=(a2+b2)*c
=(a2+b2)+c2
∴ a* (b*c) ∈ (a*b) *c
⇒ Operation * is not associative.
(iii) In Q , a* b = a+ ab
Let a, b ∈ Q
∴ a* b = a+ ab and b* a = b+ba
Therefore, a*b ≠ b*a
⇒ Operation * is not commutative
Let a,b,c ∈ Q
∴ a*(b*c) = a* (b+ bc)
= a+a(b +bc)= a+ ab + abc
and (a*b) * c = (a+ab) *c
=a+ ab + ac + abc
∴ a* (b*c) ≠ (a * b) * c
⇒ OPeration * is not associative .
(iv) In Q, a* b =(a−b)2
∴ a* b =(a−b)2
=(b−a)2= b * a
⇒ Operation * is commutative .
Let a,b,c ∈ Q
∴ a* (b*c) = a* (b−c)2
=[a−(b−c)2]2
and (a*b) *c =(a−b)2* c
=[(a−b)2−c]2
∴a*(b*c)≠(a * b)*c
⇒ Operatin * is not associative .
(v) In Q, a * b=ab4
Let a,b∈Q
∴ a * ( b*c) = a* (bc4)=a(bc4)4
(ab4)c4=(abc)*c=(a*b)*c
⇒ Operation * is associtative.(iv) In Q, a * b =ab2
Let a,b,c ∈ Q
∴ a* (b*c) =a*(bc)2
=a(bc)2=aab2c2
and (a*b) *c =(ab)2*c=ab2c2
∴ a* b (b*c) ≠ (a*b) *c
⇒ operation * is not associative .
Topper's Solved these Questions
- RELATIONS AND FUNCTIONS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Miscellaneous Exercise
19 Videos
- RELATIONS AND FUNCTIONS BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Exercise 1.3
14 Videos
- PROBABIILITYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - PROBABIILITYEXERCISE - Miscellaneous Exercise
19 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - Miscellaneous Exercise
23 Videos
Similar Questions
Knowledge Check
Operators with higher precedence are evaluated before operators with relatively lower precedence. Arrange the operators given below in order of higher precedence to lower precedence.
(i) && (ii) % (iii) ≥ (iv) ++A(iv), (i), (iii), (ii)B(iv), (iii), (ii), (i)C(iv), (ii), (iii), (i)D(i), (ii), (iii), (iv)Operators with higher precedence are evaluated before operators with relatively lower precedence. Arrange the operators given below in order of higher precedence to lower precedence.
(i) &&
(ii) %
(iii) >=
(iv) ++A(iv), (i), (iii), (ii)B(iv), (iii), (ii), (i)C(iv), (ii), (iii), (i)D(i), (ii), (iii), (iv)
Let ∗ be a binary operation on the set Q of rational numbers as follows:
(i) a∗b=a−b (ii) a∗b=a2+b2
Find which of the binary operations are commutative and which are associative
View SolutionA binary operation on a set has always the identity element.
View Solution
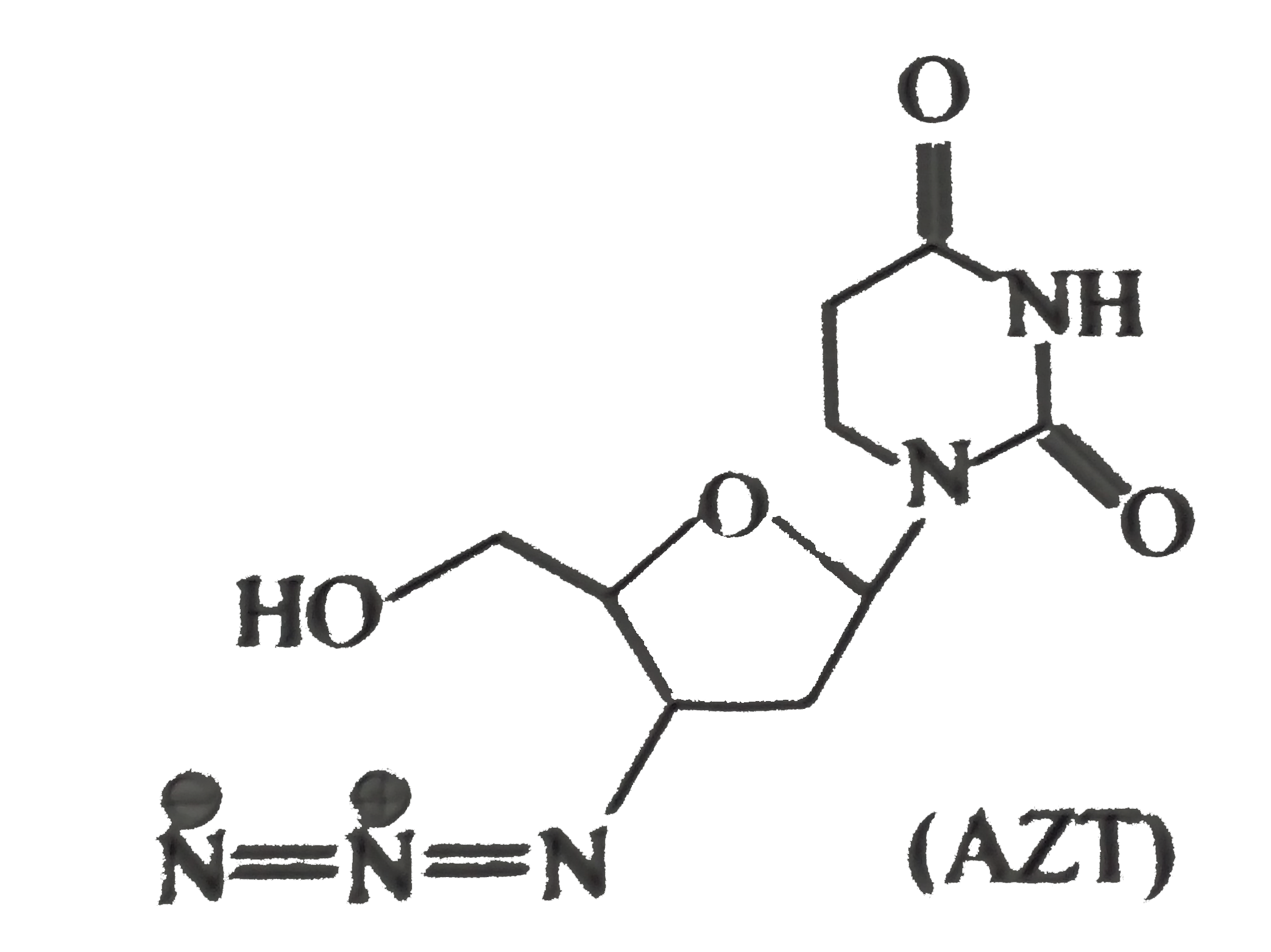
AZT structure is given above find which of the following functional groups are present in AZT.
View SolutionGiven the circuit :
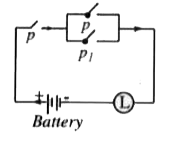
Which of the following is equivalent to the above circuit ?
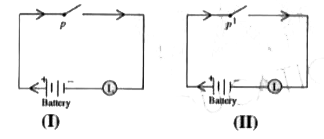
The true statement in the above is/are
View SolutionShow that zero is the identity for addition on R and 1 is the identity for multiplication on R. But there is no identity element for the operations −:R×R→Rand ÷:R⋅×R⋅→R⋅.
View SolutionFor the binary operation * on Z defined by a*b= a+b+1 the identity element is
View Solution
