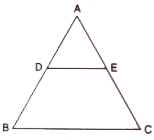
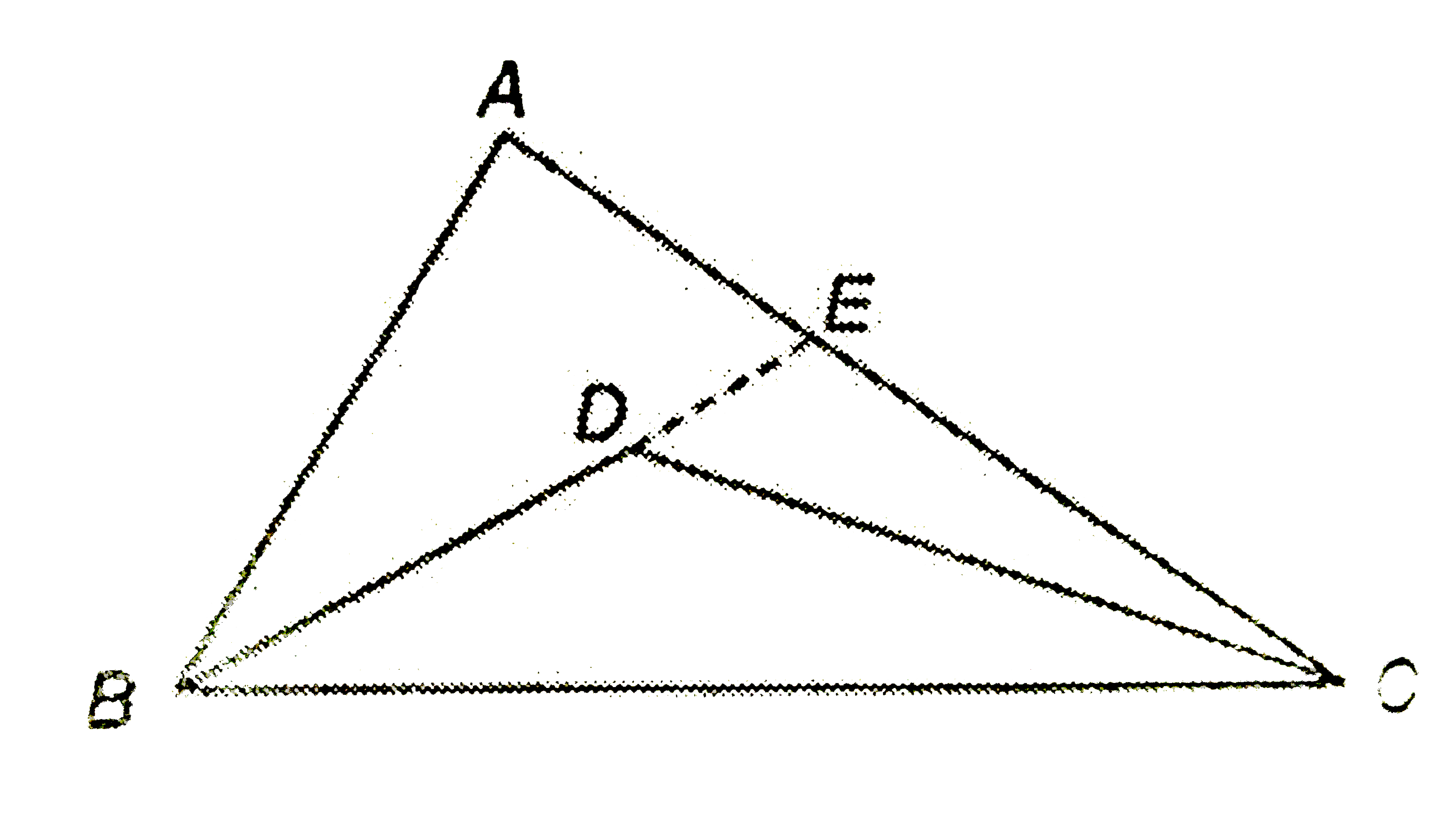
In the adjoining figure ADE and ABC are two similar triangles, point D divides AB in the raito 2:1 and point E divides AC in the ratio 1:2 . If the area of $△ A D E$ is 23 square units, then find the ar( $□ D E C B)$ .

Video Solution

Text Solution

Verified by Experts

We have
$\frac{A D}{D B} = \frac{2}{1} and \frac{A E}{E C} = \frac{1}{2}$
Let AD = 2x $\Rightarrow D B = x and let A E = y \Rightarrow E C = 2 y \Rightarrow A C = 3 y$
$\frac{A D}{D B} \neq \frac{A E}{E C}$
DEcancel||BC.
$∠ D \neq ∠ B and ∠ E \neq ∠ C$ .
But since $△ A D E and △ A B C$ are similar and $∠ A$ is common to both the triangles.
$△ A D E and △ A B C$
$∠ A = ∠ A$ (common)
and $∠ D = ∠ C$ (obvious)
$△ A D E ~ △ A C B$ (AA corollary)
$\frac{A D}{A C} = \frac{D E}{C B} = \frac{A E}{A B} \Rightarrow \frac{2 x}{3 y} = \frac{y}{3 x} \Rightarrow 6 x^{2} = 3 x y \Rightarrow 2 x = y$
$\frac{a r (△ A D E)}{a r (△ (A C B)) = \frac{A D^{2}}{A C^{2}}}$
if two triangles are similar then ratio of their areas is equal to the ratio of square of their corresponding sides)
$\frac{4 x^{2}}{9 y^{2}} = \frac{{(2 x)}^{2}}{9 y^{2}} = \frac{y^{2}}{9 y^{2}} = \frac{1}{9}$
$\frac{23}{a r (△ A C B)} = \frac{1}{9}$
$a r (△ A C B) = 23 \times 9 = 209$ sq units
$a r (square D E C B) = a r (△ A B C) - a r (△ A D E)$
207-23= 184 sq units.

Updated on:21/07/2023

|

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-TRIANGLES -Revision Exercise Long Questions

Home
Ask Doubt
Profile