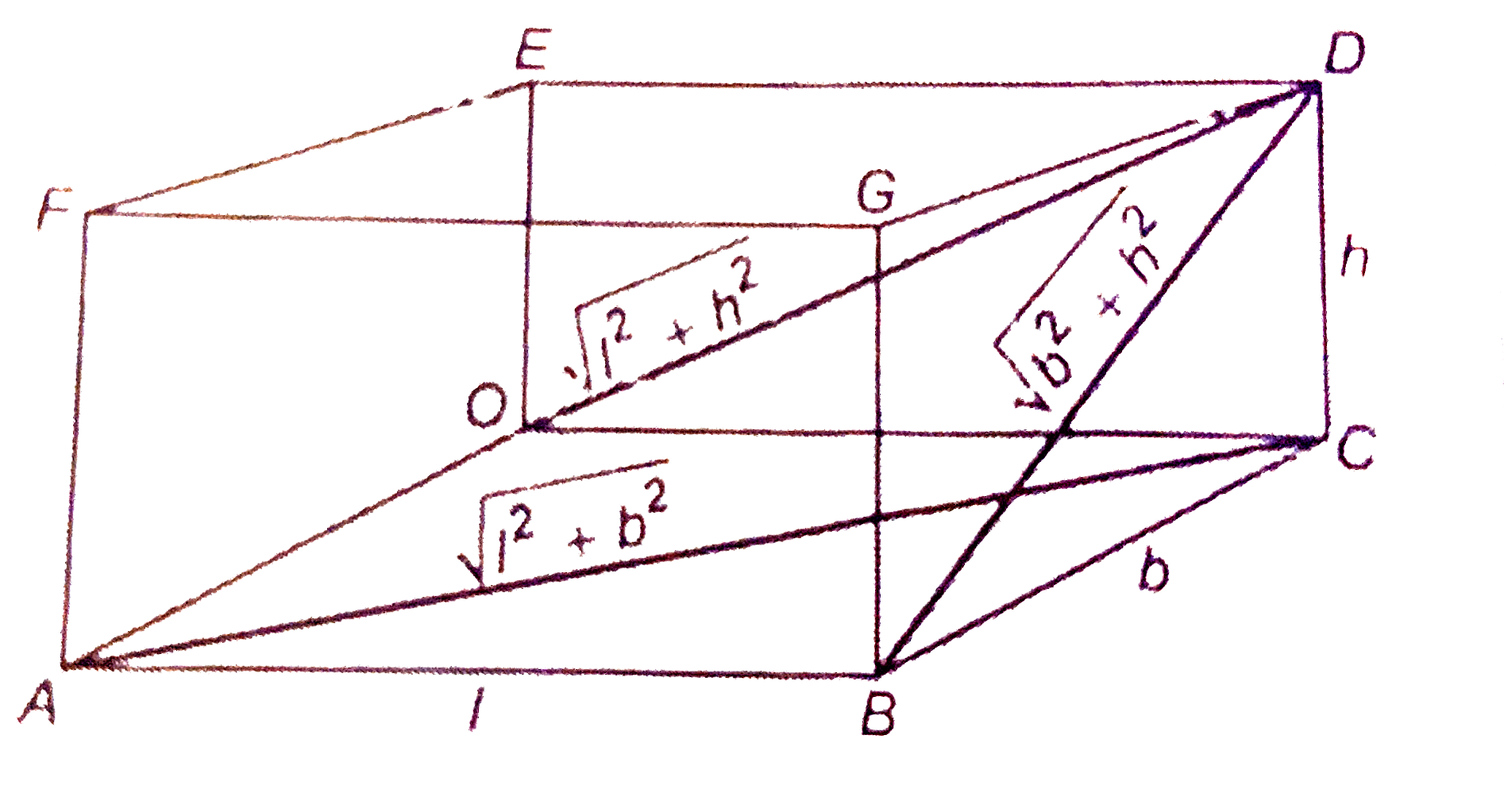
The three different face diagonals of a cuboid (rectangular parallelopipd ) have lengths 39,40 and 41 units .Find the length of the main diagonal of the cuboid which joins a pair of opposite corners.
Let l,b,h be the length
=1600..(2)
Adding (1),(2)and(3), we get
Length of main diagonal EB=
Topper's Solved these Questions
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Problems From NCERT/exemplar
10 Videos
- VOLUME AND SURFACE AREA OF SOLIDSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - VOLUME AND SURFACE AREA OF SOLIDSEXERCISE - Exercise
68 Videos
- TRIANGLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLES EXERCISE - Revision Exercise Long Questions
1 Videos
Similar Questions
The lengths of the diagonals of a rhombus are 30cm and 40cm. Find the side of the rhombus.
View SolutionTwo opposite angles of a rhombus are 60° each. If the length of each side of the rhombus is 8 cm, find the lengths of the diagonals of the rhombus.
View SolutionThe sum of the length, breadth and height of a cuboid is 38 cm and the length of its diagonal is 22 cm. Find the surface area of the cuboid.
View SolutionThe sum of length, breadth and depth of a cuboid is 19cm and the length of its diagonal is 11cm. Find the surface area of the cuboid.
View SolutionThe ends of a diagonal of a square have co-ordinates (−2,p)and(p,2). Find p, if the area of the square is 40 sq. units.
View SolutionAOBC is a rectangle whose three vertices are A(0,-3), O(0,0) and B (4,0). The length of its diagonal is__
View SolutionAOBC is a rectangle whose three vertices are A(0,-3), O(0,0) and B (4,0). The length of its diagonal is__
View SolutionThe sum of length, breadth and depth of a cuboid is 19 cm and length of its diagonal is 11 cm. Find the surface area of the cuboid.
View SolutionThe sum of length, breadth and depth of a cuboid is 19 cm and length of its diagonal is 11 cm. Find the surface area of the cuboid.
View SolutionFour identical cubes are joined end to end to form a cuboid .If the total surface area of the resulting cuboid is 648 cm2 .Find the length of edge of each cube.
View Solution
