Find the equation of the circle passing through (0, 0) and making intercepts a and b on the coordinate axes.

Video Solution

Text Solution

Verified by Experts

Let the circle passes through the origin O.
Given : OA = a and OB = b
$∴ A \equiv (a, 0) and B \equiv (0, b)$
$∵ ∠ (A O B = 90^{\circ}$
$∴$ AB is the diameter of circle.
Equation of the circle , the end points of whose diameter are $(x_{1}, y_{1}) and (x_{2}, y_{2})$ is
$(x - x_{1}) (x - x_{2}) + (y - y_{2}) (y - y_{2}) = 0$ .
$∴$ Equation of circle, the coordinates of the end points of whose diameter are (A,0) and (0,b) is
(x-a)(x-0)+(y-0)(y-b)=0
$\Rightarrow x^{2} + y^{2} - a x - b y = 0$
But the intercepts can be any direction.
So, four circles are possible whose equations are.
$x^{2} + y^{2} \pm a x \pm b y = 0$

Updated on:21/07/2023

|

Class 11 MATHS PARABOLA

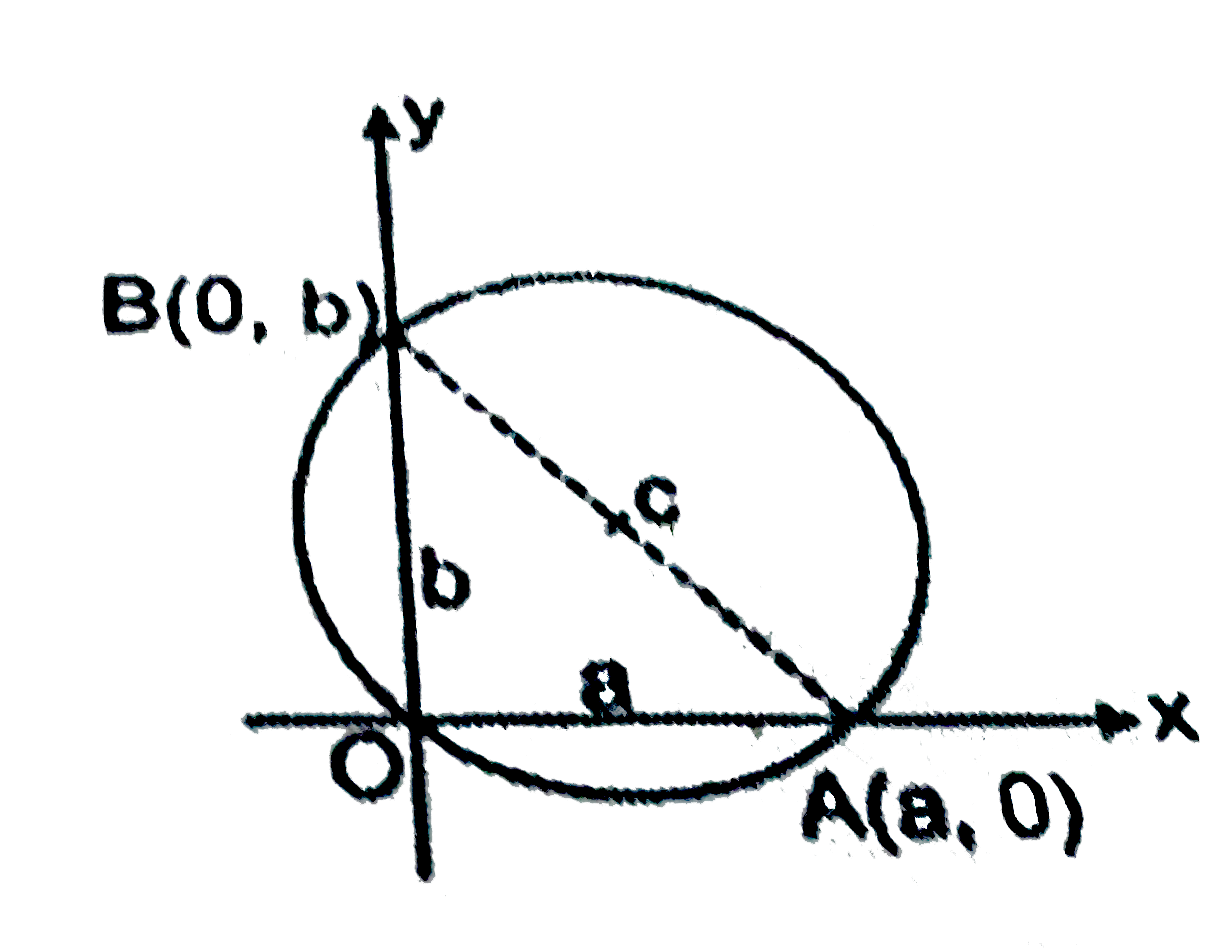
Topper's Solved these Questions

Similar Questions

Knowledge Check

Find the equation of the circle which passes through the origin and cuts off intercepts -2 and 3 from the coordinate axes .
Ax^(2) + y^(2) + 2x + 3y = 0
B $x^{2} + y^{2} + 2 x - 3 y = 0$
C $x^{2} + y^{2} - 2 x + 3 y = 0$
D $x^{2} + y^{2} - 2 x - 3 y = 0$

NAGEEN PRAKASHAN ENGLISH-CONIC SECTION-Exercise 11.1

Home
Ask Doubt
Profile