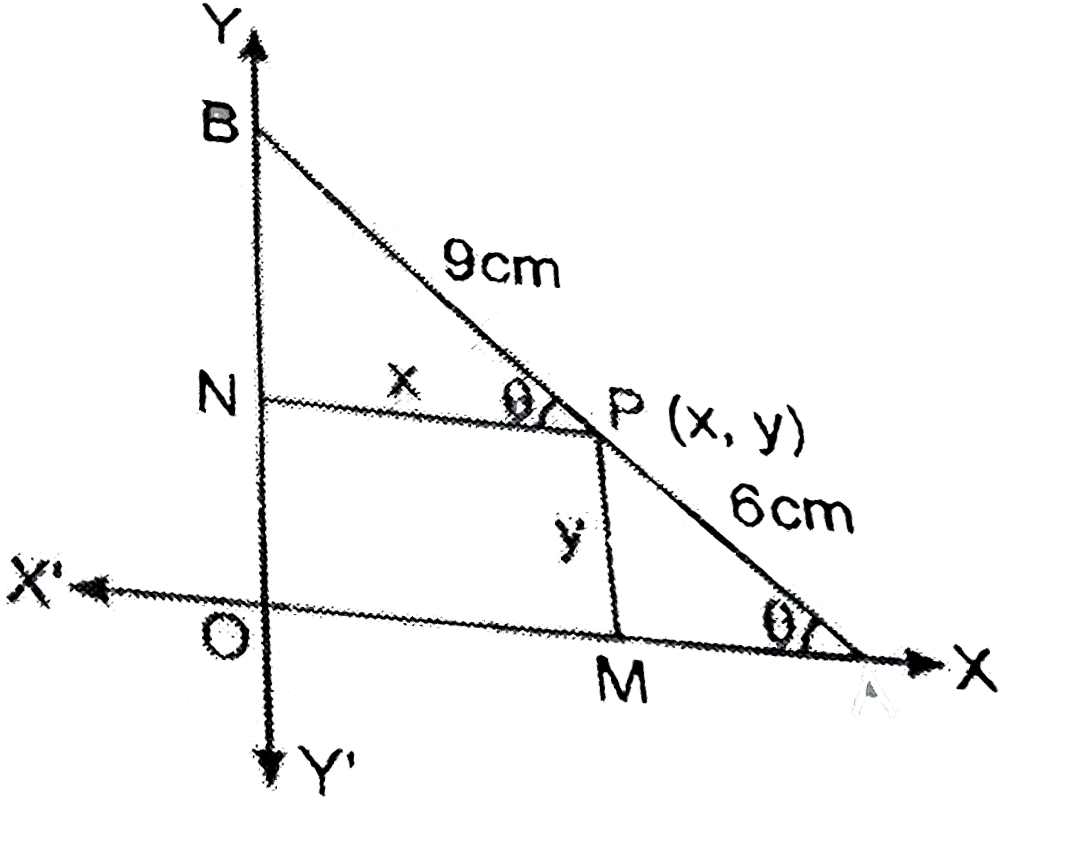
A rod AB of length 15cm rests in between two coordinate axes in such a way that the end point A lies on x−aξs and end point B lies on y−aξs . A point is taken on the rod in such a way that AP=6cm . Show that the locus of P is an ellipse. Also find its eccentricity.
Let the rod AB makes an angle θ from x-axis.
Here AB=15 cm and AP = 6 cm
⇒ BP=9cm
In ΔAPM
sinθ=y6
In ΔPBN
cosθ=x9
∵ cos2θ+sin2θ=1
⇒ (x9)2+(y6)2=1
⇒ x281+y236=1, which is the locus of point P
Topper's Solved these Questions
- CONIC SECTIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONIC SECTIONEXERCISE - Exercise 11A
37 Videos
- CONIC SECTIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONIC SECTIONEXERCISE - Exercise 11B
19 Videos
- CONIC SECTIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CONIC SECTIONEXERCISE - Miscellaneous Exercise
8 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATION BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATION EXERCISE - MISCELLANEOUS EXERCISE
20 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION OF THREE DIMENSIONAL GEOMETRYEXERCISE - Miscellaneous Exercise
6 Videos
Similar Questions
A rod AB of length 15cm rests in between two coordinate axes in such a way that the end point A lies on x−axis and end point B lies on y-axis . A point is taken on the rod in such a way that AP=6cm . Show that the locus of P is an ellipse. Also find its eccentricity.
View SolutionAB is a variable line sliding between the coordinate axes in such a way that A lies on the x-axis and B lies on the y-axis. If P is a variable point on AB such that PA=b,Pb=a , and AB=a+b, find the equation of the locus of P.
View SolutionAB is a variable line sliding between the coordinate axes in such a way that A lies on the x-axis and B lies on the y-axis. If P is a variable point on AB such that PA=b,Pb=a , and AB=a+b, find the equation of the locus of P.
View SolutionAB is a variable line sliding between the coordinate axes in such a way that A lies on the x-axis and B lies on the y-axis. If P is a variable point on AB such that PA=b,Pb=a , and AB=a+b, find the equation of the locus of P.
View SolutionA point P(x, y) moves so that the product of the slopes of the two lines joining P to the two points (-2, 1) and (6, 5) is -4. Show that the locus is an ellipse and locate its centre.
View SolutionIf a point P moves such that its distance from (a,0) is always equal to a+x-coordinate of P, show that the locus of P is y2=4ax.
View SolutionA rod of length l cm moves with its ends A (on x=-axis) and B (on y-axis) always touching the coordinae axes. Prove that the point P on the rod which divides AB in the ratio λ(≠1) is ellipse. Alos, find the eccentricity of the ellipse.
View SolutionA rod of length / slides with its ends on two perpendicular lines. Find the locus of its mid-point.
View SolutionA(−1,0)andB(2,0) are two given points. A point M is moving in such a way that the angle B in the triangle AMB remains twice as large as the angle A. Show that the locus of the point M is a hyperbola. Fnd the eccentricity of the hyperbola.
View SolutionA variable line through the point (65,65) cuts the coordinates axes in the point AandB. If the point P divides AB internally in the ratio 2:1, show that the equation to the locus of P is :
View Solution
