The diagram shows the cross-section of eight identical iron balls touching each other on a horizontal surface.

If the volume of a ball is 9π2cm3, then what should be the minimum length and depth of a box so that all the balls can be placed in it ?
Volume of each ball =43πr3
∴43πr3=9π2 (given)
∴r3=278⇒r=32 (taking cube root)
∴ Diameter of each ball = 3 cm
∴ Length AB=8× diameter of ball =8×3=24cm
and depth of box = diameter of ball = 3 cm.
So, minimum length and depth of box should be 24 cm and 3 cm respectively.
Topper's Solved these Questions
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Problems From NCERT/exemplar
24 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Exercise 13a
30 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - Revision Exercise
12 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Revision Exercise (long Answer Type Question)
8 Videos
Similar Questions
Three identical metal balls each of radius r are placed touching each other on a horizontal surface such that an equilateral triangle is formed, when the center of three balls are joined. The center of mass of system is located at the
View SolutionTwo identical balls each of mass m interconnected by a small light inextensible string are kept on a smooth horizontal surface. One of the balls is pushed towards the other with a speed v0 find the loss of K.E. of the ball. What will be the final velocities of the balls ? (e=1).

View SolutionFigure shows a light rod of length l rigidly attached to a small heavy block at one end and a hook at the other end. The system is released from rest with the rod in a horizontal position. There is a fixed smooth ring at a depth h below the initial position of the hook and the hook gets into the ring as it reaches there. What should be the minimum value of h so that the block moves in a complete circle about the ring?

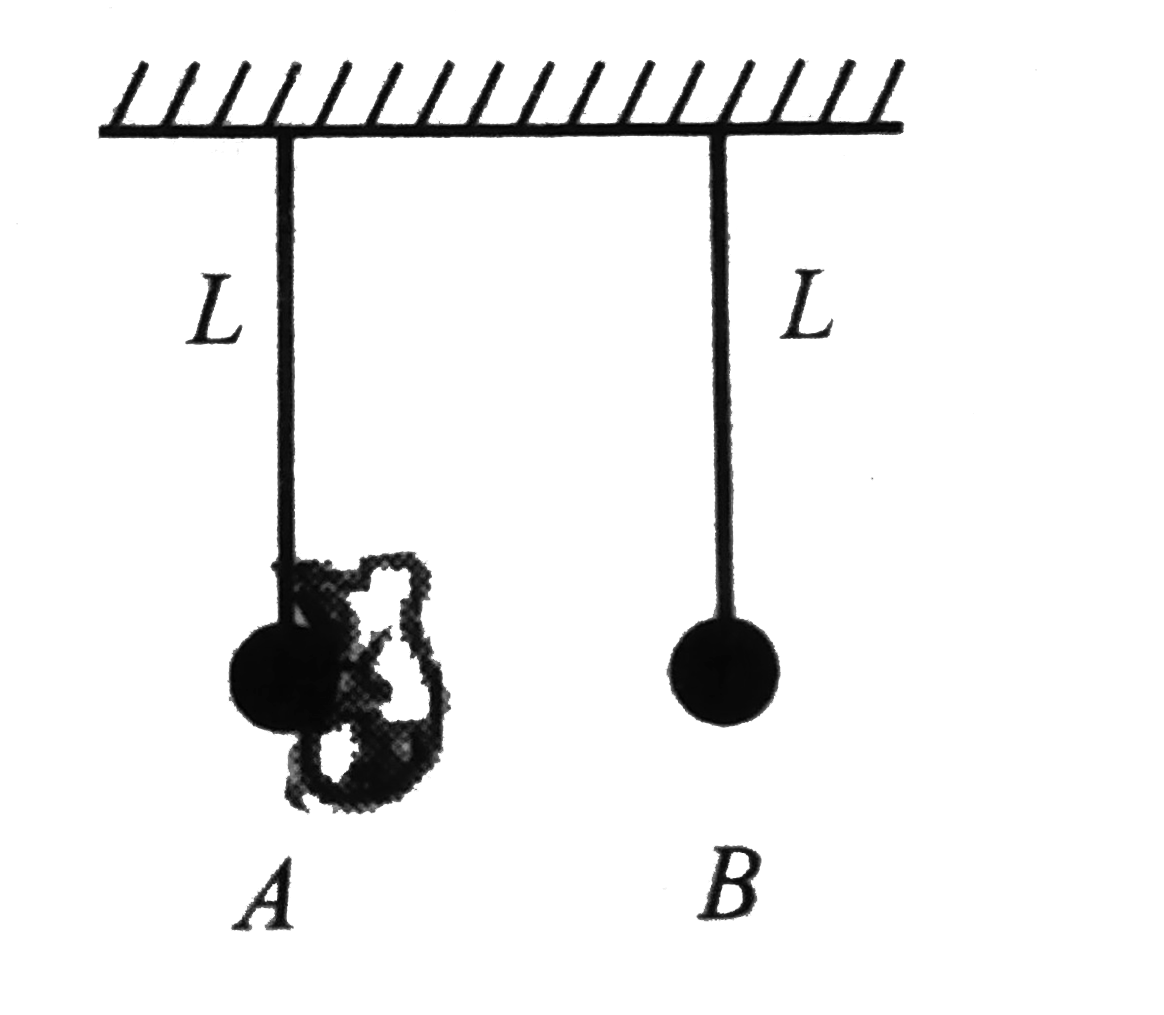
View SolutionAn insect jumps from ball A onto ball B, which are suspended from inextensible light strings each of length L=8cm. The mass of each ball and insect is same. What should be the minimum relative velocity (in ms−1) of jump of insect w.r.t. ball A, if both the balls manage to complete the full circle?
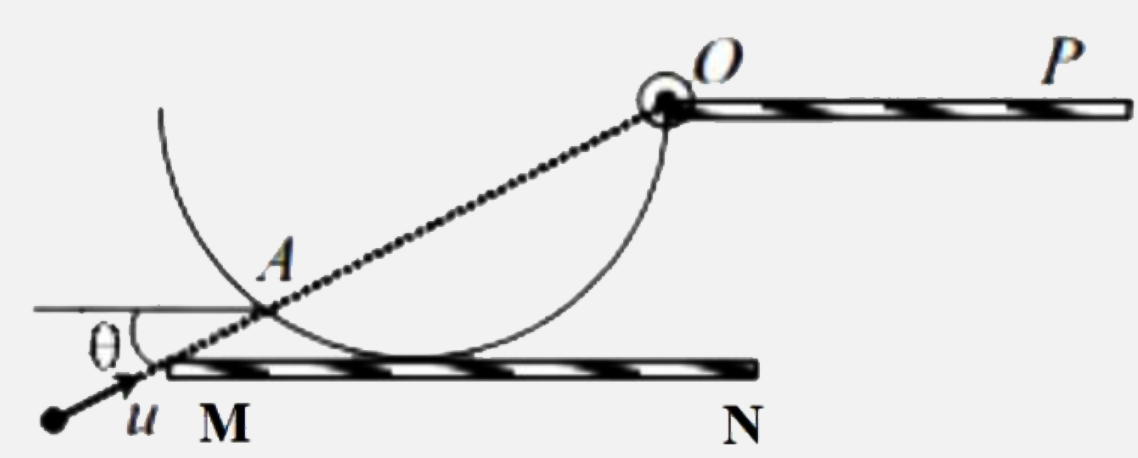
View SolutionThe diagram shows a hemispherical shell of mass m and radius R is hinged at point of placed on a horizontal surface. A ball of mass strikes the shell at point A ( as shown in the figure ) moving with velocity u inclined at an angle θ=tan−1(12) and then it stops . For the given shell to reach horizontal surface OP what minimum speed u is required ?
View SolutionAn object is placed at a distance of 30 cm from a converging lens of focal length 15 cm. A normal eye (near point 25 cm, far point infinity) is placed close to the lens on the other side. (a) Can the eye see the object clearly? (b) What should be the minimum separation between the lens and the eye so that the eye can clearly see the object? c. Can a diverging lens, placed in contact with the converging lens, help in seeing the object clearly when the eye is close to the lens?
View SolutionSome identical balls are arranged in rows to form an equilateral triangle. The first row consists of one ball, the second row consists of row balls and so on. If 99 more identical balls are added to the total number of balls used in forming the equilateral triangle, then all these balls can be arranged in a square whose each side contains exactly 2 balls less than the number of balls each side of the triangle contains. Then, the number of balls used to form the equilateral triangle is
View SolutionIn the figure shown, the two identical balls of mass M and radius R each, are placed in contact with each other on the frictionless horizontal surface. The third ball of mass M and radius R/2, is coming down vertically and has a velocity =v0 when it simultaneously hits the two balls and itself comes to rest. Then, each of the two bigger balls will move after collision with a speed equal to

View SolutionA small ball of mass 2×10−3kg, having a charge 1μC, is suspended by a string of length 0.8m. Another identical ball having the same charge is kept at the point of suspension. Determine the minimum horizontal velocity that should be imparted to the lower ball so that it can make a complete revolution.
View SolutionTwo identical balls AandB each of mass 0.1kg are attached to two identical mass less is springs. The spring-mass system is constrained to move inside a right smooth pipe bent in the form of a circle as shown in figure . The pipe is fixed in a horizontal plane. The center of the balls can move in a circle of radius 0.06m. Each spring has a natural length of 0.06πm and force constant 0.1N/m. Initially, both the balls are displaced by an angle θ=π/6 radians with respect to diameter PQ of the circle and released from rest.
a. Calculate the frequency of oscillation of the ball B.

View Solution
