Solve : a(x+y)+b(x−y)=a2−ab+b2, a(x+y)−b(x−y)=a2+ab−b2
Given equations can be written as
ax+ay+bx−by=a2−ab+b2
⇒(a+b)x+(a−b)y=a2−ab+b2 ....(1)
and ax+ay−bx+by=a2+ab+b2
⇒(a−b)x+(a+b)y=a2+ab+b2 ....(2)
For equations (1) and (2) by cross multiplication method, we have
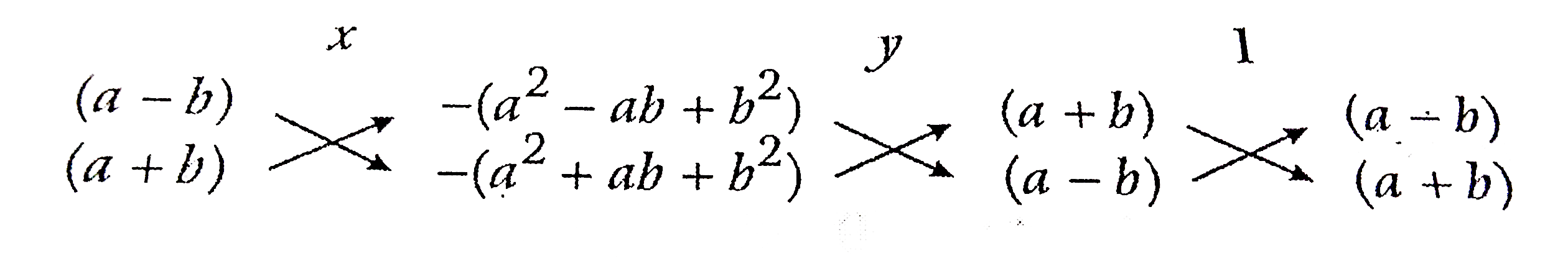
x(a−b)×[−a2+ab+b2]−(a+b)×[−(a2−ab+b2)]
=y[−(a2−ab+b2)]×(a−b)−[−(a2+ab+b2)×(a+b)]=1(a+b)(a+b)−(a−b)(a−b)
implies x−(a3−b3)+(a3+b3)
=y−(a3−a2b+ab2−a2b+ab2−b3)+(a3+a2b+ab2+a2b+ab2+b3)=1(a+b)2−(a−b)2
implies x2b3=y2a2b−2ab2+b3+2a2b+2ab2+b3=14ab
implies x2b3=y4a2b+2b3=14ab
implies x2b3=y2b(2a2+b2)=14ab
when x2b3=14ab⇒x=2b34ab⇒x=b22a
and y2b(2a2+b2)=14ab⇒y=2b(2a2+b2)4ab⇒y=2a2+b22a
Hence, x=b22ay=2a2+b22a⎫⎪⎬⎪⎭ is the required solution.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Exercise 3a18videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Exercise 3A8videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Revision Exercise Long Answer Questions5videos
INTRODUCTION TO TRIGONOMETRY
- BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - POLYNOMIALSEXERCISE - Revision Exercise Long Answer Questions4videos
POLYNOMIALS
Similar Questions
Solve: x+y=a+b ; ax−by=a2−b2
View Solutionx+y=a+b,ax−by=a2−b2
View SolutionSolve xa+yb=1 and a(x−a)−b(y+b)=2a2+b2.
View SolutionSolve the following system of equations in x and y (a−b)x+(a+b)y=a2−2ab−b2, (a+b)(x+y)=a2+b2
View SolutionSolve : ax−by=0ab2x+a2by=a2+b2
View SolutionSolve for 'x' and 'y': (a−b)x+(a+b)y=a2−b2−2aband(a+b)(x+y)=a2+b2
View Solution(a−b)x+(a+b)y=a2−2ab−b2 , (a+b)(x+y)=a2+b2 find x and y
View SolutionSolve: ax+by=a−b, bx−ay=a+b
View SolutionIf the origin is shifted to the point (aba−b,0) without rotation, then the equation (a−b)(x2+y2)−2abx=0 becomes
View SolutionThe foci of hyperbola xy=((a^2 + b^2)/(4))aregivenby(A)x = y = +- ((a^2 + b^2)/(4a))(B)x = y = +- ((a^2 + b^2)/(4b))(C)x = y = +- ((a^2 + b^2)/(2a))(D)x = y = +- ((a^2 + b^2)/(2b))
View Solution
