A circle is touching the side BC of a △ABC at point P and touching AB and AC produced at Q and R respectively. Prove that AQ=12(perimeter of △ABC).
To prove that AQ=12 (perimeter of triangle ABC), we will follow these steps:
Step 1: Define the points and segments
Let A,B,C be the vertices of triangle ABC. The incircle of the triangle touches side BC at point P, and it touches the extensions of sides AB and AC at points Q and R respectively.
Step 2: Use the properties of tangents
From the properties of tangents to a circle, we know that the lengths of tangents drawn from an external point to a circle are equal. Therefore, we can write:
- AQ=AP (let this be equation 1)
- BP=BQ (let this be equation 2)
- CR=CP (let this be equation 3)
Step 3: Express the sides of the triangle in terms of tangents
Let:
- AP=s−a where s is the semi-perimeter of triangle ABC and a=BC
- BQ=s−b where b=AC
- CR=s−c where c=AB
Step 4: Write the perimeter of triangle ABC
The perimeter P of triangle ABC is given by:
P=AB+BC+AC=a+b+c
The semi-perimeter s is:
s=a+b+c2
Step 5: Relate AQ to the semi-perimeter
From the definitions of AQ,BP,CR and the semi-perimeter, we have:
AQ=s−a
Substituting s:
AQ=a+b+c2−a=b+c−a2
Step 6: Express the perimeter in terms of AQ
Now, we can express the perimeter in terms of AQ:
P=2AQ+a
Thus, we can rearrange to find:
AQ=12(P−a)
Step 7: Final expression for AQ
Since AQ is equal to the semi-perimeter minus the side a:
AQ=12(a+b+c)=12P
Conclusion
Thus, we have proved that:
AQ=12(perimeter of triangle ABC)
Let A,B,C be the vertices of triangle ABC. The incircle of the triangle touches side BC at point P, and it touches the extensions of sides AB and AC at points Q and R respectively.
From the properties of tangents to a circle, we know that the lengths of tangents drawn from an external point to a circle are equal. Therefore, we can write:
- AQ=AP (let this be equation 1)
- BP=BQ (let this be equation 2)
- CR=CP (let this be equation 3)
Let:
- AP=s−a where s is the semi-perimeter of triangle ABC and a=BC
- BQ=s−b where b=AC
- CR=s−c where c=AB
The perimeter P of triangle ABC is given by:
P=AB+BC+AC=a+b+c
The semi-perimeter s is:
s=a+b+c2
From the definitions of AQ,BP,CR and the semi-perimeter, we have:
AQ=s−a
Substituting s:
AQ=a+b+c2−a=b+c−a2
Now, we can express the perimeter in terms of AQ:
P=2AQ+a
Thus, we can rearrange to find:
AQ=12(P−a)
Since AQ is equal to the semi-perimeter minus the side a:
AQ=12(a+b+c)=12P
Thus, we have proved that:
AQ=12(perimeter of triangle ABC)
Topper's Solved these Questions
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Problems From NCERT/exemplar
11 Videos
- CIRCLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLESEXERCISE - Exercise
32 Videos
- ARITHMETIC PROGRESSIONBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question
5 Videos
- CO-ORDINATE GEOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions
10 Videos
Similar Questions
In the given figure the sides AB, BE and CA of triangle ABC touch a circle with centre O and radius r at P,Q and R respectively.
Prove that : (i)AB+CQ=AC+BQ

View SolutionThe incircle of an isoceles triangle ABC, with AB=AC, touches the sides AB,BC and CA at D,E and F respecrively. Prove that E bisects BC.
View SolutionD is a point in side BC of triangle ABC. If AD>AC, show that AB>AC.
View SolutionIn the given triangle P, Q and R are the mid points of sides AB, BC and AC respectively. Prove that triangle PQR is similar to triangle ABC.

View SolutionOn the sides AB and AC of triangle ABC, equilateral triangles ABD and ACE are drawn. Prove that :
∠CAD=∠BAE
View SolutionIn a triangle ABC,D is the mid - point of BC, AD is produced upto E so that DE = AD.
Prove that :
AB=EC
View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

Find the equation of the line AC.
View SolutionIn isosceles triangle ABC, D is a point on the base BC produced. Prove that AD>AB.

View SolutionIn the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.
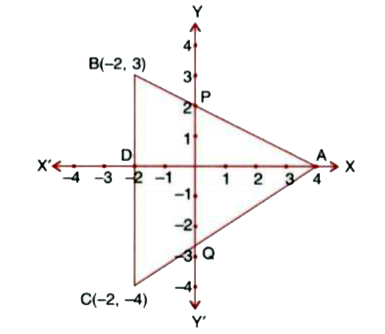
Write the co-ordinates of A.
View SolutionThe radius of the circle touching two sides AB and AC of a triangle ABC and having its center on BC is equal to………………..
View Solution
