Show that the products of the corresponding terms of the sequence a,ar,ar2,…arn−1 and A,AR,AR2,…ARn−1 from a G.P. and find the common ratio.
The correct Answer is:N/a
To show that the products of the corresponding terms of the sequences a,ar,ar2,…,arn−1 and A,AR,AR2,…,ARn−1 form a geometric progression (G.P.) and to find the common ratio, we can follow these steps:
Step 1: Write down the sequences
The first sequence is:
- a,ar,ar2,…,arn−1
The second sequence is:
- A,AR,AR2,…,ARn−1
Step 2: Find the products of corresponding terms
Now, we will find the product of the corresponding terms from both sequences:
- The first term: a⋅A
- The second term: ar⋅AR=aA⋅rR
- The third term: ar2⋅AR2=aA⋅r2R2
- Continuing this way, the kth term will be: ark−1⋅ARk−1=aA⋅rk−1Rk−1
Thus, the products of corresponding terms form the sequence:
- aA,aA⋅rR,aA⋅r2R2,…,aA⋅rn−1Rn−1
Step 3: Identify the common ratio
To show that this sequence is a G.P., we need to find the common ratio between consecutive terms.
The first term is aA and the second term is aA⋅rR. The common ratio R can be calculated as follows:
R=Second termFirst term=aA⋅rRaA=rR
Now, let's check the ratio between the second term and the first term:
Second term=aA⋅rR
Third term=aA⋅r2R2
The common ratio between the second and third terms is:
Third termSecond term=aA⋅r2R2aA⋅rR=r2R2rR=rR
Thus, the common ratio between any two consecutive terms is rR.
Conclusion
The products of the corresponding terms of the sequences a,ar,ar2,…,arn−1 and A,AR,AR2,…,ARn−1 form a G.P. with a common ratio of rR.
The first sequence is:
- a,ar,ar2,…,arn−1
- A,AR,AR2,…,ARn−1
Now, we will find the product of the corresponding terms from both sequences:
- The first term: a⋅A
- The second term: ar⋅AR=aA⋅rR
- The third term: ar2⋅AR2=aA⋅r2R2
- Continuing this way, the kth term will be: ark−1⋅ARk−1=aA⋅rk−1Rk−1
- aA,aA⋅rR,aA⋅r2R2,…,aA⋅rn−1Rn−1
To show that this sequence is a G.P., we need to find the common ratio between consecutive terms.
R=Second termFirst term=aA⋅rRaA=rR
Second term=aA⋅rR
Third term=aA⋅r2R2
The common ratio between the second and third terms is:
Third termSecond term=aA⋅r2R2aA⋅rR=r2R2rR=rR
The products of the corresponding terms of the sequences a,ar,ar2,…,arn−1 and A,AR,AR2,…,ARn−1 form a G.P. with a common ratio of rR.
Topper's Solved these Questions
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9.4
10 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Miscellaneous Exercise
32 Videos
- SEQUENCE AND SERIESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SEQUENCE AND SERIESEXERCISE - Exercise 9.2
18 Videos
- RELATIONS AND FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE
12 Videos
- SETSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SETSEXERCISE - MISC Exercise
16 Videos
Similar Questions
Show that the products of the corresponding terms of the sequences a, ar, ar2,.., arn−1 and A, AR, AR2, , ARn−1 form a G.P. and find the common ratio.
View SolutionShow that the products of the corresponding terms of the sequences a, ar,ar2,...,arn−1and A,AR,AR2,...,ARn−1,form a G.P, and find the common ratio.
View Solution
Knowledge Check
Choose the compounds below that ar aromatic :
A B
B C
C D
D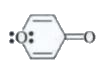
Which one of the following compounds is most reactive for ArSN2 reaction ?
A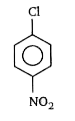 B
B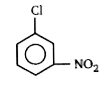 C
C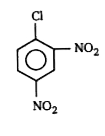 D
D
Prove that the sum of n terms of the reciprocals of the terms of the series a,ar,ar2,… is 1−rna(1−r)rn−1
View SolutionBoth fibrous roots and stilt roots ar found in
View SolutionHe, Ar, Ne (increasing order of number of electron shells)
View SolutionAmong the following
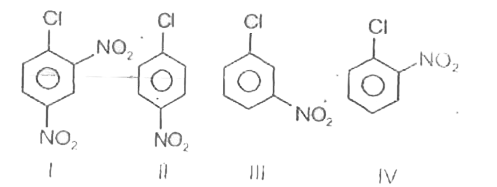
The correct order of reactivity towards ArSN mechanism is
View SolutionThe size of the iso-electronic species Cl−,Ar and Ca2+ is affected by:
View SolutionSound is transmitted from middle ar to internal ear due to
View Solution
